모형
Minitab은 반응 범주가 K개인 모형에 대해 K – 1개의 로짓 함수를 계산합니다. 예를 들어 범주가 3개(1, 2, 3)인 반응에는 2개의 로짓 함수(기준 사건 = 3)가 있습니다.
공식
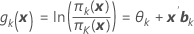
표기법
| 용어 | 설명 |
|---|---|
| gk(x) | 로짓 연결 함수 |
| θk | k번째 개별 반응값 범주와 연관된 상수 |
| xk | 예측 변수의 벡터 |
| bk | k번째 로짓 함수와 연관된 계수의 벡터 |
요인/공변량 패턴
데이터 집합의 단일 요인/공변량 값 집합에 대해 설명합니다. Minitab에서는 각 요인/공변량 패턴에 대한 사건 확률, 잔차 및 기타 진단 측도를 계산합니다.
예를 들어 데이터 집합에 성별 및 인종 요인과 나이 공변량이 포함되어 있는 경우, 이런 예측 변수의 조합에는 피실험자 수만큼 많은 공분산 패턴이 포함될 수 있습니다. 데이터 집합에 각각 2개 수준에서 코드화된 인종과 성별 요인만 포함되어 있는 경우, 가능한 요인/공변량 패턴은 4개뿐입니다. 데이터를 빈도나 성공, 시행 또는 실패 횟수로 입력할 경우 각 행에 요인/공변량 패턴이 하나씩 포함됩니다.
사건 확률
π로 나타냅니다. 범주 1, 2, 3을 포함하는 3 범주 모형(기준 사건 3)의 경우, 조건부 확률은 다음과 같습니다.
공식
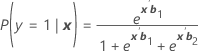
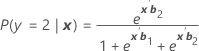
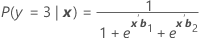
그리고 사건 확률은 다음과 같습니다.
πk(x) = P(y = k|x), k = 1, 2, 3. 각 확률은 2(p + 1)개 모수 벡터 b' = (b'1, b'2)의 함수입니다.
로그 우도
로그 우도 함수를 극대화하여 b의 최적 값을 구합니다. 모형에 반응 범주가 3개인 경우(기준 = 3) 로그 우도 함수는 다음과 같습니다.
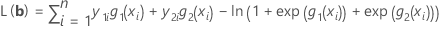
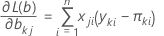
최대 우도 추정치는 이 방정식을 0으로 설정하고 b의 해를 구하여 얻습니다.
표기법
| 용어 | 설명 |
|---|---|
| k | 1, 2 |
| j | 0, 1, 2, ..., p |
| p | 상수 계수를 포함하지 않는 모형의 계수 수 |
| πki | πk(xi), 각 과목에 대해 x0i 포함 |
계수
모수 추정치라고도 하는 최대 우도 추정치입니다. K개의 개별 반응 값이 있는 경우, Minitab은 각 예측 변수에 대해 K – 1개의 모수 집합을 추정합니다. 효과는 기준 사건과 비교한 반응 범주에 따라 다릅니다. 각 로짓은 한 반응 범주 대 기준 사건 로그 승산의 차이 추정치를 제공합니다. K – 1 방정식의 모수는 다른 모든 반응 범주 쌍을 사용하여 로짓에 대한 모수를 결정합니다.
추정 계수는 최대 우도 추정과 동등한 반복 재가중 최소 제곱법을 사용하여 계산합니다.1,2
참고 문헌
- D.W. Hosmer and S. Lemeshow (2000). Applied Logistic Regression. 2nd ed. John Wiley & Sons, Inc.
- P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
계수 표준 오차
추정 계수의 정확도를 나타내는 점근적 표준 오차. 표준 오차가 작을수록 추정값이 더 정확합니다.
자세한 내용은 [1]과 [2]를 참조하십시오.
- A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
- P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
Z는 예측 변수가 반응과 유의한 연관이 있는지 확인하기 위해 사용합니다. Z의 절대값이 클수록 관계가 유의함을 나타냅니다. p-값은 정규 분포에서 Z가 어디에 위치하는지 나타냅니다.
공식
Z = βi / 표준 오차
상수 공식은 다음과 같습니다.
Z = θk / 표준 오차
표본이 작은 경우, 우도 비율 검정이 더 신뢰할 수 있는 유의도 검정일 수 있습니다.
p-값(P)
귀무 가설을 기각하거나 받아들이는 가설 검정에서 사용됩니다. p-값은 귀무 가설이 참인 경우 최소한 실제로 계산된 값만큼 극단적인 검정 통계량을 얻을 확률입니다. 일반적으로 사용되는 p-값에 대한 컷오프 값은 0.05입니다. 예를 들어, 검정 통계량의 계산된 p-값이 0.05보다 작으면 귀무 가설을 기각합니다.
승산비
예측 변수와 반응값 사이의 관계를 해석하는 데 유용합니다.
승산비(q)는 음수가 아닌 모든 숫자일 수 있습니다. 승산비 1은 비교 기준으로 사용됩니다. θ = 1이면 반응값과 예측 변수 사이에 연관성이 없습니다. θ > 1이면 요인의 기준 수준(또는 계량형 예측 변수의 더 높은 수준)에 대한 비교 반응 사건의 승산이 더 높습니다. θ < 1이면 요인의 기준 수준(또는 계량형 예측 변수의 더 높은 수준)에 대해 비교 반응 사건의 승산이 더 적습니다. 값이 1에서 멀수록 연관성이 더 강함을 나타냅니다.
예를 들어 반응 범주가 3개(1, 2, 3)이고 예측 변수가 1개인 모형의 경우 승산비는 결과 범주 k에 대한 범주 대 기준 사건으로 사용되는 결과 범주(이 예에서는 3)의 승산을 지정합니다. 다음은 a와 b라는 2개 수준이 있는 예측 변수에 대한 승산비의 공식입니다.
공식
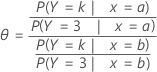
표기법
| 용어 | 설명 |
|---|---|
| k | 결과 범주 |
신뢰 구간
공식
βi 에 대한 큰 표본 신뢰 구간은 다음과 같습니다.
β i + Zα /2*(표준 오차)
확률 비율의 신뢰 구간을 구하려면 신뢰 구간의 하한 및 상한을 멱승하십시오. 구간은 예측 변수의 모든 단위 변동에 대해 확률이 하락할 수 있는 범위를 정합니다.
표기법
| 용어 | 설명 |
|---|---|
| α | 유의 수준 |
분산-공분산 행렬
p +1 × (K – 1) 차원을 포함하는 정방 행렬입니다. 각 계수의 분산은 대각 셀에 있고 각 계수 쌍의 공분산은 해당 대각 외 셀에 있습니다. 분산은 계수 제곱의 표준 오차입니다.
분산-공분산 행렬은 점근적이며 정보 역행렬의 마지막 반복으로부터 얻습니다. 이차 부분 도함수 행렬은 공분산 행렬을 구하기 위해 사용됩니다.
표기법
| 용어 | 설명 |
|---|---|
| p | 예측 변수의 수 |
| K | 반응의 범주 수 |
Pearson
모형이 데이터에 적합한 정도를 나타내는 Pearson 잔차에 기초한 요약 통계량. Pearson은 공분산의 개별 값 수가 관측치 수와 거의 같은 경우 유용하지 않지만, 공분산 수준이 같은 반복 관측치가 있는 경우 유용합니다. χ2 검정 통계량이 높고 p-값이 낮을수록 모형이 데이터에 적합하지 않을 수 있음을 나타냅니다.
공식은 다음과 같습니다.
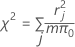
여기서 r = Pearson 잔차, m = j번째 요인/공분산 패턴의 시행 횟수, 그리고 π0 = 비율 가설 값입니다.
이탈도
모형이 데이터에 적합한 정도를 나타내는 이탈도 잔차에 기초한 요약 통계량. 이탈도는 공분산의 개별 값 수가 관측치 수와 거의 같은 경우 유용하지 않지만, 공분산 수준이 같은 반복 관측치가 있는 경우에는 유용합니다. D 값이 더 높고 p-값이 더 낮을수록 모형이 데이터에 적합하지 않을 수 있음을 나타냅니다. 검정에 대한 자유도는 (k - 1)*J − (p)이며, 여기서 k는 반응값의 숫자 범주이고 J는 개별 요인/공분산 패턴의 수이며 p는 계수의 수입니다.
공식은 다음과 같습니다.
D =2 Σ yik log p ik− 2 Σ yik log π ik
여기서 πik = k번째 범주에 대한 i번째 관측치의 확률입니다.
