레버리지(Hi)
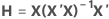
i번째 관측치의 레버리지는 H의 i번째 대각 원소 hi입니다. hi가 크면 i번째 관측치가 비정상적인 예측 변수(X1i, X2i, ..., Xpi)를 가집니다. 즉, 예측 변수 값이 평균 벡터 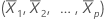 에서 멀리 떨어져 있으며, Mahalanobis 거리를 사용합니다.
에서 멀리 떨어져 있으며, Mahalanobis 거리를 사용합니다.
레버리지 값은 0과 1 사이입니다. Minitab에서는 3p/n 또는 0.99 중 작은 수 이상의 레버리지를 갖는 관측치를 식별합니다. 이러한 관측치는 비정상 관측치 표에 X로 표시되어 있습니다. 일반적으로 레버리지가 큰 값을 조사합니다.
표기법
| 용어 | 설명 |
|---|---|
| X | 설계 행렬 |
| hi | 모자 행렬의 i번째 대각 원소 |
| p | 상수를 포함한 모형의 항 수 |
| n | 관측치 수 |
검증을 통한 레버리지(Hi)
수식

가중치 회귀 분석의 경우 수식에는 가중치가 포함됩니다.
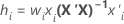
표기법
| 용어 | 설명 |
|---|---|
| X | design matrix for the rows in the training data set or the folds that act as the training data set |
| xi | the vector of predictors in the i번째 validation row |
| wi | weight for the i번째 validation row |
Cook의 거리
추정된 회귀 계수에 대한 모든 관측치에 걸친 결합된 영향력을 나타내는 전반적인 측도 D. Minitab에서는 레버리지 값과 표준화 잔차를 사용하여 D를 계산하고, 관측치가 x-값과 y-값 모두에 대해 비정상인지 여부를 고려합니다. D 값이 큰 관측치는 특이치일 가능성이 있습니다.
공식
Cook의 거리는 i번째 관측치를 포함하여 계산한 적합치와 i번째 관측치를 포함하지 않고 계산한 적합치 사이의 거리입니다. Minitab에서는 관측치가 제외될 때마다 새 회귀 방정식을 적합하지 않고 Cook의 거리를 계산합니다. 계산 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| ei | i번째 잔차 |
| hi | 다음의 i번째 대각 원소: 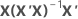 |
| p | 상수를 포함한 모형 모수의 수 |
| s 2 | 평균 제곱 오차 |
| b | 계수 벡터 |
| b(i) | i번째 관측치를 삭제한 후 계산한 계수 벡터 |
| X | 설계 행렬 |
DFITS
레버리지와 스튜던트화 잔차(외적 스튜던트화 t 잔차) 값을 관측치가 얼마나 비정상적인지 나타내는 하나의 전체 측도로 결합합니다. DFITS는 회귀 및 분산 분석 모형의 적합치에 대한 각 관측치의 영향을 측정합니다. DFITS 값이 큰 관측치는 특이치일 가능성이 있습니다.
DFITS는 각 관측치를 데이터 집합에서 제거하고 모형을 다시 적합시킬 때 적합치가 바뀌는 표준 편차의 개수를 대략적으로 나타냅니다. Minitab에서는 관측치가 제외될 때마다 새 회귀 방정식을 적합하지 않고 DFITS를 계산할 수 있습니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| ei | i번째 잔차 |
| hi | 다음의 i번째 대각 원소: 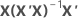 |
| X | 설계 행렬 |
 | i 번째 적합 반응 |
 | i번째 관측치를 포함하지 않고 계산한 적합치 |
| MSE (i) | i번째 관측치를 포함하지 않고 계산한 평균 제곱 오차 |
| n | 관측치 수 |
| p | 모형 모수의 수 |
분산 팽창 인수(VIF)
VIF는 각 예측 변수를 나머지 예측 변수에 회귀하고 R2 값을 참고하여 얻을 수 있습니다.
공식
예측 변수가 xj인 경우 VIF는 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| R2( xj) | 반응 변수가 xj이고 예측 변수가 모형의 나머지 항인 결정 계수 |
Durbin-Watson 통계량
인접한 두 오차항 사이의 상관 계수가 0인지 확인하여 잔차에 자기 상관이 있는지 여부를 검정합니다. 이 검정에서는 오차들이 일차 자기 회귀 과정에 의해 생성된다는 가정을 기초로 합니다. Minitab에서는 관측치가 시간 순서처럼 의미 있는 순서로 정렬되어 있다고 가정합니다.

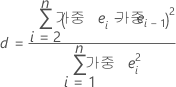
표기법
| 용어 | 설명 |
|---|---|
| ei | ith 잔차 |
| ei -1 | 이전 관측치의 잔차 |
| n | 관측치 수 |
