원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
제곱합(SS)
행렬 항에서 여러 제곱합에 대한 공식은 다음과 같습니다.
Minitab에서는 SS 회귀 분석 또는 SS 처리 성분을 순차 제곱합과 수정 제곱합을 모두 사용하여 각 항에 의해 설명되는 변동량으로 세분화합니다.
표기법
| 용어 | 설명 |
|---|---|
| b | 계수의 벡터 |
| X | 설계 행렬 |
| Y | 반응 값의 벡터 |
| n | 관측치 수 |
| J | 1의 n x n 행렬 |
순차 제곱합
Minitab에서는 변동의 SS 회귀 분석 또는 처리 성분을 각 요인의 순차 제곱합으로 세분화합니다. 순차 제곱합은 모형에 요인 또는 예측 변수를 입력한 순서에 따라 다릅니다. 순차 제곱합은 이전에 요인을 입력한 경우 SS 회귀 분석에서 한 요인만으로 설명되는 부분을 나타냅니다.
예를 들어 X1, X2, X3 등 요인 또는 예측 변수가 세 개인 모형의 경우 X2의 순차 제곱합은 X1이 모형에 포함된 상태에서 X2에 의해 설명되는 분산의 정도를 나타냅니다. 요인의 다른 순서를 얻으려면 분석을 반복하고 다른 순서로 요인을 입력합니다.
자유도(DF)
모형의 각 구성 요소에 대한 자유도는 다음과 같습니다.
| 변동 출처 | DF |
|---|---|
| 회귀 분석 | p |
| 오류 | n – p – 1 |
| 합계 | n – 1 |
데이터가 특정 기준을 충족하고 모형에 하나 이상의 계량형 예측 변수나 둘 이상의 범주형 예측 변수가 포함된 경우, Minitab은 적합성 결여 검정에 자유도를 사용합니다. 기준은 다음과 같습니다.
- 데이터에는 예측 변수 값이 같은 관측치가 여러 개 있습니다.
- 데이터에는 모형에 없는 추가 항을 추정하기 위한 올바른 점이 있습니다.
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| p | 모형의 계수 수(상수 제외) |
Adj MS – 회귀 분석
회귀 분석의 평균 제곱(MS)에 대한 공식은 다음과 같습니다.
표기법
| 용어 | 설명 |
|---|---|
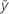 | 평균 반응 |
 | i번째 적합 반응 |
| p | 모형의 항 수 |
Adj MS – 오차
오차의 평균 제곱(MS 오차 또는 MSE로 줄이고 s2로 표기함)은 적합 회귀선 주변의 분산입니다. 공식은 다음과 같습니다.
표기법
| 용어 | 설명 |
|---|---|
| yi | i번째 관측된 반응 값 |
 | ith번째 적합 반응 |
| n | 관측치 수 |
| p | 상수를 제외한 모형 내 계수의 수 |
Adj MS – 합계
평균 제곱(MS) 합계 공식은 다음과 같습니다.
표기법
| 용어 | 설명 |
|---|---|
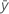 | 평균 반응 |
| yi | i번째 관측 반응 값 |
| n | 관측치 수 |
F-값
F-통계량 공식은 다음과 같습니다.
- F(회귀분석)
-
- F(항)
-
- F(적합성 결여)
-
표기법
| 용어 | 설명 |
|---|---|
| MS 회귀 분석 | 현재 모형이 설명하는 반응 변동의 측도. |
| MS 오차 | 모형이 설명하지 않는 변동의 측도. |
| MS 항 | 모형의 나머지 항을 고려한 후 항이 설명하는 변동 양의 측도. |
| MS 적합성 결여 | 모형에 더 많은 항을 추가하여 모형화할 수 있는 반응의 변동 측도. |
| MS 순수 오차 | 반복된 반응 데이터의 변동 측도. |
p-값 – 분산 분석표
p-값은 자유도(DF)가 다음과 같은 F 분포에서 계산되는 확률입니다.
- 분자 DF
- 검정의 항에 대한 자유도의 합
- 분모 DF
- 오차에 대한 자유도
공식
1 − P(F ≤ fj)
표기법
| 용어 | 설명 |
|---|---|
| P(F ≤ f) | F-분포의 누적분포함수 |
| f | 검정에 대한 f-통계량 |
순수 오차 적합성 결여 검정
순수 오차 적합성 결여 검정을 계산하기 위해 Minitab은
- 반복실험의 각 집합 내 평균으로부터 반응의 제곱 편차의 합을 계산한 다음 더하여 순수 오차 제곱합(SS PE)을 생성합니다.
- 순수 오차 평균 제곱
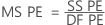
여기서 n = 관측치의 수이고 m = 고유한 x-수준 조합의 수입니다.
- 적합성 결여 제곱합
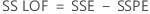
- 적합성 결여 평균 제곱
- 검정 통계량
큰 F-값과 작은 p-값은 모형이 적절하지 않다는 것을 나타냅니다.
p-값 - 적합성 결여 검정
이 p-값은 이러한 데이터에서 추정할 수 있는 모형에 없는 모든 항에 대한 계수가 0이라는 귀무 가설의 검정에 대한 것입니다. p-값은 자유도(DF)가 다음과 같은 F 분포의 확률입니다.
- 분자 DF
- 적합성 결여 검정의 자유도
- 분모 DF
- 순수 오차에 대한 자유도
공식
1 − P(F ≤ fj)
표기법
| 용어 | 설명 |
|---|---|
| P(F ≤ fj) | F-분포의 누적분포함수 |
| fj | 검정에 대한 f-통계량 |
