이 항목의 내용
지수 모임 및 연결 함수
기존 선형 모형을 일반화 선형 모형으로 확장하려면 지수 모임 분포와 연결 함수의 두 가지 부분이 필요합니다.
지수 모임
첫 부분에서는 선형 모형을 지수 모임이라는 큰 분포 모임의 구성원인 반응 변수로 확장합니다. 분포의 지수 모임에 속한 구성원은 관측된 반응에 대해 다음과 같은 일반적인 형식의 확률 분포 함수를 갖습니다.
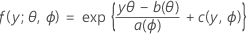
여기서 a(∙), b(∙) 및 c(∙)는 반응 변수의 분포에 따라 다릅니다. 모수 θ는 종종 정규 모수라고 하는 위치 모수이며, ϕ는 산포 모수라고 합니다. a(ϕ) 함수는 일반적으로 a(ϕ)= ϕ/ ω 형식이며, 여기서 ω는 알려진 상수이거나 관측치마다 다를 수 있는 가중치일 수 있습니다. (Minitab에서 가중치에 a(ϕ) 함수가 제공되면 적절하게 조정됩니다.)
지수 모임의 구성원은 이산형 분포이거나 계량형 분포일 수 있습니다. 지수 모임의 구성원인 계량형 분포의 예는 정규 및 감마 분포입니다. 지수 모임의 구성원인 이산형 분포의 예는 이항 및 포아송 분포입니다. 아래 표에는 이러한 분포 특성들이 나와 있습니다.
| 분포 | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| 정규 분포 | σ2 | θ2/2 | φω |  |
| 이항 분포 | 1 | 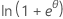 |
φ/ω | -ln(y!) |
| 포아송 분포 | 1 | exp(θ) | φ/ω |  |
연결 함수
두 번째 부분은 연결 함수입니다. 연결 함수는 i 번째 관측치의 반응 평균을 다음과 같은 형식으로 선형 예측 변수에 연결합니다.
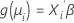
기존 선형 모형은 연결 함수가 항등원 함수인 이 일반 공식의 특별한 경우입니다.
두 번째 부분에서 선택하는 연결 함수는 첫 부분의 지수 모임의 특정 분포에 따라 결정됩니다. 특히 지수 모임의 각 분포에는 정규 연결 함수라는 특수 연결 함수가 있습니다. 이 연결 함수는 θ가 정규 모수인 g (μi) = Xi'β= θ 방정식을 충족합니다. 정규 연결 함수의 결과는 몇 가지 바람직한 모형의 통계적 속성입니다. 적합도 통계량은 다른 연결 함수를 사용하여 적합치를 비교하는 데 사용할 수 있습니다. 일부 연결 함수는 경험적인 이유로 또는 원칙에 있어 특별한 의미를 가지고 있기 때문에 사용할 수도 있습니다. 예를 들어, 로짓연결함수의 장점은 승산비의 추정치를 제공한다는 것입니다. 또 다른 예는 노밋 연결 함수에서는 이원 범주로 분류된 정규 분포를 따르는 기본 변수가 있다고 가정한다는 것입니다.
Minitab은 각 모형 등급에 대해 세 가지 연결 함수를 제공합니다. 서로 다른 연결 함수를 사용하여 다양한 데이터에 충분히 적합한 모형을 찾을 수 있습니다.
이항 분포 모형의 경우, 연결 함수는 로짓, 노밋(프로빗) 및 곰핏(보 로그-로그)입니다. 이 연결 함수들은 누적 로지스틱 분포 함수의 역함수(로짓), 표준 누적 정규 분포 함수의 역함수(노밋), 그리고 Gompertz 분포 함수의 역함수(곰핏)입니다. 로짓은 이항 분포 모형에 대한 정규 연결 함수이므로, 로짓이 기본 연결 함수입니다.
포아송 분포 모형의 경우 연결 함수는 자연 로그, 제곱근 및 항등원 함수입니다. 자연 로그는 포아송 분포 모형에 대한 정규 연결 함수이므로, 자연 로그가 기본 연결 함수입니다.
아래에는 연결 함수가 요약되어 있습니다.
| 모형 | 이름 | 연결 함수, g(μi) |
| 이항 분포 | 로짓 | 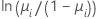 |
| 이항 분포 | 노밋(프로빗) | 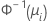 |
| 이항 분포 | 곰핏(보 로그-로그) |  |
| 포아송 분포 | 자연 로그 | 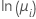 |
| 포아송 분포 | 제곱근 |  |
| 포아송 분포 | 항등원 | 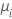 |
표기법
| 용어 | 설명 |
|---|---|
| μi | i 번째 행의 평균 반응 |
| g(μi) | 연결 함수 |
| X | 예측 변수의 벡터 |
| β | 예측 변수와 연관된 계수의 벡터 |
 | 정규 분포의 역 누적분포함수 |
요인/공변량 패턴
데이터 집합의 단일 요인/공변량 값 집합에 대해 설명합니다. Minitab에서는 각 요인/공변량 패턴에 대한 사건 확률, 잔차 및 기타 진단 측도를 계산합니다.
예를 들어 데이터 집합에 성별 및 인종 요인과 나이 공변량이 포함되어 있는 경우, 이런 예측 변수의 조합에는 피실험자 수만큼 많은 공분산 패턴이 포함될 수 있습니다. 데이터 집합에 각각 2개 수준에서 코드화된 인종과 성별 요인만 포함되어 있는 경우, 가능한 요인/공변량 패턴은 4개뿐입니다. 데이터를 빈도나 성공, 시행 또는 실패 횟수로 입력할 경우 각 행에 요인/공변량 패턴이 하나씩 포함됩니다.
이항 로지스틱 모형 적합에 대한 내부 가중치
수식
- 로짓
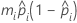
- 노밋

- 곰핏

표기법
| 용어 | 설명 |
|---|---|
| mi | the number of trials for the i번째 row |
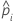 | the predicted probability for the design point in a binary logistic model |
| yi | the number of events for the i번째 row |
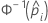 | the inverse cumulative distribution function of the standard normal distribution for the predicted probability in a binary logistic model |
Minitab이 이항 로지스틱 모형 적합의 회귀 분석에서 높은 상관 관계가 있는 예측 변수를 제거하는 방법
rij를 Xi 및 Xj 행렬과 관련된 현재 제거된 행렬의 원소로 설정합니다.
변수는 한 번에 하나씩 추가되거나 제거됩니다. Xk는 현재 rkk ≥ 1(기본값이 0.0001인 공차)인 모형에 포함되지 않은 독립 변수인 경우 추가할 수 있으며, 또한 현재 모형에 포함된 각 변수 Xj에 대해,

- Minitab에서는 상관 행렬 R에 대해 SWEEP 방법을 수행하고 X1 … Xp를 랜덤 변수인 것처럼 처리합니다.
- 연속형 예측 변수의 경우, Minitab에서는 원소 rkk를 공차와 비교합니다. rkk ≥ 공차이며 여기서 k = 1 ~ p입니다.
- 현재 모형에 있는 각 변수 Xj 에 대해 Minitab에서는 (rjj – rjk * (rkj / rkk)) * 공차 ≤ 1임을 확인합니다.
참고
여기서 rkk, rjk, rjj는 k 단계 SWEEP 연산 후 Xj 및 Xk 변수에 해당하는 대각 및 비대각 원소입니다.
- 그렇지 않은 경우, 예측 변수는 검정을 통과하지 못하며 모형에서 제거됩니다.
참고
기본 공차 값은 8.8e–12입니다.
참고
TOLERANCE 하위 명령을 GZLM 세션 명령과 함께 사용하여 Minitab에서 다른 예측 변수와 높은 상관 관계가 있는 예측 변수를 모형에 유지하도록 할 수 있습니다. 그러나 공차를 낮추는 것은 위험하며 숫자가 부정확해질 수 있습니다.
