원하는 방법 또는 공식을 선택하십시오.
이 항목의 내용
적합치 및 예측 값
연결 함수는 모형마다 다릅니다. 예측 값을 계산하려면 모형에 대한 연결 함수의 역함수를 구하십시오. 역함수는 다음 표에 있습니다.
| 모형 | 연결 함수 | 예측 공식 |
|---|---|---|
| 이항 분포 | 로짓 | 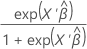 |
| 이항 분포 | 노밋 | 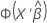 |
| 이항 분포 | 곰핏 |  |
| 포아송 분포 | 자연 로그 | 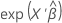 |
| 포아송 분포 | 제곱근 | 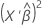 |
| 포아송 분포 | 항등원 | 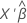 |
표기법
| 용어 | 설명 |
|---|---|
| exp(·) | 지수 함수 |
| Φ(·) | 정규 분포의 누적분포함수 |
| X' | 예측할 점의 벡터 전치 |
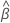 | 추정 계수 벡터 |
적합치 및 예측의 표준 오차
일반적으로 맞춤의 표준 오차는 다음과 같은 형태를 가립니다.
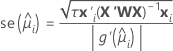
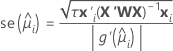
다음 수식은 서로 다른 링크 함수에 대한 맞춤의 표준 오류를 제공합니다.
- 로짓
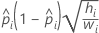
- 노밋
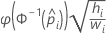
- 곰핏

테이블의 수식에 적용되는 다음 관계를 참고하십시오.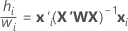
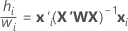
여기서 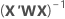 는 유효성 검사에 대한 테스트 데이터 집합이 있는 경우에만 학습 데이터에서 입니다.
는 유효성 검사에 대한 테스트 데이터 집합이 있는 경우에만 학습 데이터에서 입니다.
표기법
| 용어 | 설명 |
|---|---|
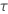 | 1, for the binomial and Poisson models |
| xi | the vector of a design point |
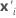 | the transpose of xi |
| X | the design matrix |
| W | the weight matrix |
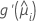 | the first derivative of the link function evaluated at 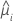 |
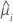 | the predicted mean response |
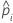 | the predicted probability for the design point in a binary logistic model |
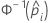 | the inverse cumulative distribution function of the standard normal distribution for the predicted probability in a binary logistic model |
 | the probability density function of the standard normal distribution |
적합치 및 예측에 대한 신뢰 한계
신뢰 한계에는 Wald 근사 방법이 사용됩니다. 다음은 100 (1에 대한 일반적인 공식입니다 - α양측 신뢰 구간의 경우

다음 표는 다양한 모형 유형 및 링크 함수에 대한 특정 수식을 제공합니다.
| 유형 | 링크 | 적합치의 표준 오차 |
|---|---|---|
| 이항 로지스틱 | 로짓 | 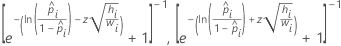 |
| 이항 로지스틱 | 노밋 | 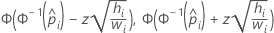 |
| 이항 로지스틱 | 곰핏 | 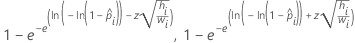 |
| 포아송 | 로그 | 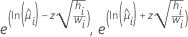 |
| 포아송 | 제곱근 | 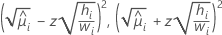 |
| 포아송 | 항등원 |  |
테이블의 수식에 적용되는 다음 관계를 참고하십시오.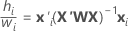
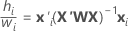
여기서 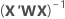 는 유효성 검사에 대한 테스트 데이터 집합이 있는 경우에만 학습 데이터에서 입니다.
는 유효성 검사에 대한 테스트 데이터 집합이 있는 경우에만 학습 데이터에서 입니다.
표기법
| 용어 | 설명 |
|---|---|
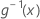 | the inverse of the link function evaluated at x |
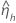 | 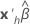 |
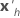 | the transpose of the vector of the predictors |
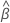 | the vector of estimated coefficients |
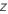 | the value of the inverse cumulative distribution function for the normal distribution evaluated at  |
| α | the significance level |
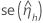 |  |
| X | the design matrix |
| W | the weight matrix |
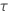 | 1, for binomial and Poisson models |
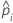 | the predicted probability for the design point in a binary logistic model |
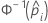 | the inverse cumulative distribution function of the standard normal distribution for the predicted probability in a binary logistic model |
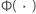 | the cumulative distribution function of the standard normal distribution |
