계수
계수의 최대우도 추정치를 구하는 방법은 두 가지입니다. 한 방법은 계수에 대한 우도 함수를 직접 극대화하는 방법입니다. 이 식은 계수에서 비선형입니다. 다른 방법은 Minitab이 계수의 추정을 얻기 위해 사용하는 방법입니다 반복 재가중치 최소 사각형 (IRWLS) 접근 방식을 사용하는 것입니다. McCullagh와 Nelder1은 두 가지 방법이 동등하다는 것을 보여줍니다. 그러나 반복 재가중 최소 제곱 방법은 이행하기가 더 쉽습니다. 자세한 내용은 1을 참조하십시오.
K-fold 교차 유효성 검사의 경우 1단계 근사치 방법
많은 교차 유효성 검사 접기가 있는 일부 대형 샘플 설계의 경우 Minitab은 교차 유효성 검사 알고리즘에서 1단계 근사치 방법을 사용하여 계산 시간을 줄입니다(Pregibon2 및 Williams3참조). 이러한 설계의 경우 IRWLS 알고리즘과 접기학습모델에 적합한 학습 모델을 전체 수렴에 맞추기보다는 접기에 대한 교차 검증 통계는 알고리즘의 첫 번째 반복 단계로부터 회귀 매개 변수에서 비롯됩니다.
다음 표에서는 1단계 근사치에서 교차 유효성 검사 통계를 받는 디자인을 보여 주었습니다.
| 표본 크기(n) | 설계 행렬의 열 수(p) | 접기 수(k) |
|---|---|---|
| 200 < n ≤ 500 | 150 < p ≤ 300 | k > 200 |
| p > 300 | k > 100 | |
| 500 < n ≤ 1000 | 100 < p ≤ 300 | k > 300 |
| p > 300 | k > 150 | |
| 1000 < n ≤ 10,000 | p ≤ 50 | k > 1,000 |
| 50 < p ≤ 200 | k > 200 | |
| 200 < p ≤ 400 | k > 50 | |
| p > 400 | k > 10 | |
| 10,000 < n ≤ 50,000 | p ≤ 50 | k > 200 |
| 50 < p ≤ 200 | k > 100 | |
| p > 200 | k > 20 | |
| 50,000 < n ≤ 100,000 | p ≤ 50 | k > 100 |
| 50 < p ≤ 150 | k > 50 | |
| p > 150 | k > 20 | |
| n > 100,000 | p의 모든 값 | k > 100 |
1단계 근사치 알고리즘
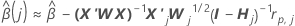
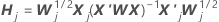
표기법
| 용어 | 설명 |
|---|---|
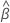 | 전체 데이터 집합에 적합한 예상 계수 |
| X | 전체 데이터 집합에 대한 설계 행렬 |
| X' | 전체 데이터 집합에 대한 설계 행렬의 횡방향 |
| W | 전체 데이터 집합의 중량 행렬 |
| X'j | jth 접기의 데이터에 대한 설계 매트릭스 |
| Wj | jth 접기의 데이터에 대한 중량 행렬 |
| Ⅰ | 단위 행렬 |
| rp, j | jth fold의 데이터에 대한 전체 데이터 집합에 대한 모델에서 Pearson 잔류의 벡터 |
[1] P. 맥컬라와 제이 에이 엘더 (1989). 일반화 선형 모델,2nd Ed., 채프먼 & 홀 / CRC, 런던.
[2] D. 프레기본 (1981). 물류 회귀 진단. The Annals of Statistics, 9(4), 705-724.
[3] D. A. 윌리엄스 (1987). 편차 및 단일 케이스 삭제, 응용 통계, 36(2), 181-191을 사용하여 일반화 선형 모델 진단.
계수 표준 오차
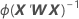
W는 대각 요소가 다음 공식에 의해 정해지는 대각 행렬입니다.
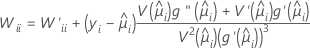
설명

이 분산-공분산 행렬은 Fisher의 정보 행렬이 아닌 관측된 Hessian 행렬에 기반을 두고 있습니다. Minitab에서는 관측된 Hessian 행렬을 사용하는데, 결과로 생성된 모형이 조건적 평균 오규격에 대해 더 로버스트하기 때문입니다.
정규 연결을 사용할 경우 관측된 Hessian 행렬과 Fisher의 정보 행렬은 동일합니다.
표기법
| 용어 | 설명 |
|---|---|
| yi | i 번째 행에 대한 반응 값 |
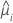 | i 번째 행에 대한 추정 평균 반응 |
| V(·) | 아래 표에 제공된 분산 함수 |
| g(·) | 연결 함수 |
| V '(·) | 분산 함수의 일차 도함수 |
| g'(·) | 연결 함수의 일차 도함수 |
| g''(·) | 연결 함수의 이차 도함수 |
분산 함수는 모형에 따라 다릅니다.
| 모형 | 분산 함수 |
| 이항 분포 | 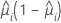 |
| 포아송 분포 | 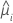 |
자세한 내용은 [1] 및 [2]에서 확인하십시오.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
Z-통계량은 예측 변수가 반응과 유의한 관련이 있는지 확인하기 위해 사용합니다. Z의 절대값이 상대적으로 크면 관계가 유의함을 나타냅니다. 공식은 다음과 같습니다.
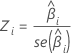
표기법
| 용어 | 설명 |
|---|---|
| Zi | 표준 정규 분포의 검정 통계량 |
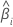 | 추정 계수 |
 | 추정 계수의 표준 오차 |
표본이 작은 경우 우도 비율 검정이 더 신뢰성이 높은 유의도 검정일 수 있습니다. 우도 비율 p-값은 이탈도 표에 있습니다. 표본 크기가 충분히 크면 Z 통계량에 대한 p-값은 우도 비율 통계량에 대한 p-값에 근사합니다.
p-값(P)
귀무 가설을 기각하거나 받아들이는 가설 검정에서 사용됩니다. p-값은 귀무 가설이 참인 경우 최소한 실제로 계산된 값만큼 극단적인 검정 통계량을 얻을 확률입니다. 일반적으로 사용되는 p-값에 대한 컷오프 값은 0.05입니다. 예를 들어, 검정 통계량의 계산된 p-값이 0.05보다 작으면 귀무 가설을 기각합니다.
이항 로지스틱 회귀 분석에 대한 승산비
승산비는 이항 반응이 포함된 모형에 대해 로짓 연결 함수를 선택하는 경우에만 제공됩니다. 이 경우 승산비는 예측 변수와 반응 간의 관계를 해석하는 데 있어 유용합니다.
승산비(τ)는 음수가 아닌 숫자입니다. 승산비 = 1은 비교 기준으로 사용됩니다. τ = 1이면 반응과 예측 변수 간에 연관성이 없습니다. τ < 1이면 요인의 기준 수준(또는 계량형 예측 변수)에 대한 사건의 확률이 더 높습니다. τ > 1이면 요인의 기준 수준(또는 계량형 예측 변수)에 대한 사건의 확률이 더 작습니다. 값이 1에서 멀리 떨어질수록 더 강한 연관도를 나타냅니다.
참고
공변량 또는 요인이 1개인 이항 로지스틱 회귀 모형의 경우 추정된 승산비는 다음과 같습니다.
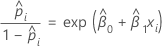
지수 관계는 β에 대한 해석을 제공합니다. x가 한 단위 증가할 때마다 확률이 eβ1씩 증가합니다. 승산비는 exp(β1)와 같습니다.
예를 들어, β가 0.75인 경우 승산비는 exp(0.75) = 2.11입니다. 이는 x가 한 단위 증가할 때마다 승산비가 111% 증가한다는 것을 나타냅니다.
표기법
| 용어 | 설명 |
|---|---|
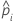 | 데이터의 i번째 행에 대해 추정된 성공 확률 |
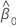 | 추정된 절편 계수 |
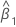 | 예측 변수 x에 대해 추정된 계수 |
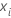 | i번째 행에 대한 데이터 점 |
신뢰 구간
추정 계수의 큰 표본 신뢰 구간은 다음과 같습니다.
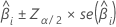
이항 로지스틱 회귀 분석의 경우, Minitab은 승산비에 대한 신뢰 구간을 제공합니다. 승산비의 신뢰 구간을 구하려면 신뢰 구간의 하한 및 상한을 멱승하십시오. 신뢰 구간은 예측 변수의 모든 단위 변동에 대해 승산비가 하락할 수 있는 범위를 정합니다.
표기법
| 용어 | 설명 |
|---|---|
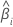 | i 번째 계수 |
 | 에서 표준 정규 분포의 역 누적 확률 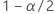 |
 | 유의 수준 |
 | 추정 계수의 표준 오차 |
분산-공분산 행렬
d가 예측 변수의 수 더하기 1인 d x d 행렬. 각 계수의 분산은 대각 셀에 있고 각 계수 쌍의 공분산은 해당 대각 외 셀에 있습니다. 분산은 계수 제곱의 표준 오차입니다.
분산-공분산 행렬은 정보 행렬의 역행렬의 마지막 반복에서 나옵니다. 분산-공분산 행렬의 형식은 다음과 같습니다.
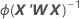
W는 대각 요소가 다음 공식에 의해 정해지는 대각 행렬입니다.

설명

이 분산-공분산 행렬은 Fisher의 정보 행렬이 아닌 관측된 Hessian 행렬에 기반을 두고 있습니다. Minitab에서는 관측된 Hessian 행렬을 사용하는데, 결과로 생성된 모형이 조건적 평균 오규격에 대해 더 로버스트하기 때문입니다.
정규 연결을 사용할 경우 관측된 Hessian 행렬과 Fisher의 정보 행렬은 동일합니다.
표기법
| 용어 | 설명 |
|---|---|
| yi | i 번째 행에 대한 반응 값 |
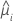 | i 번째 행에 대한 추정 평균 반응 |
| V(·) | 아래 표에 제공된 분산 함수 |
| g(·) | 연결 함수 |
| V '(·) | 분산 함수의 일차 도함수 |
| g'(·) | 연결 함수의 일차 도함수 |
| g''(·) | 연결 함수의 이차 도함수 |
분산 함수는 모형에 따라 다릅니다.
| 모형 | 분산 함수 |
| 이항 분포 | 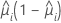 |
| 포아송 분포 | 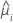 |
자세한 내용은 [1] 및 [2]에서 확인하십시오.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
