Minitab® 지원

이항 로지스틱 모형 적합의 진단 측도에 대한 방법 및 공식

Minitab 에 대해 자세히 알아보기
원하는 방법 또는 공식을 선택하십시오.

이 항목의 내용

Pearson 잔차

적합하지 않은 요인/공변량 패턴을 탐지하기 위해 사용할 수 있는 Pearson 카이-제곱의 요소. Minitab에서는 i 번째 요인/공변량 패턴에 대한 Pearson 잔차를 저장합니다. 공식은 다음과 같습니다.

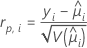
표기법

용어설명
yii 번째 요인/공변량 패턴에 대한 반응 값
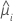i 번째 요인/공변량 패턴에 대한 적합치
V에서 모형의 분산 함수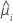

분산 함수는 모형에 따라 다릅니다.

모형 분산 함수
이항 분포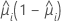
포아송 분포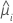

표준화 및 외적 스튜던트화 Pearson 잔차

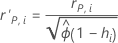
적합하지 않은 요인/공변량 패턴을 탐지하기 위해 사용합니다. Minitab에서는 i 번째 요인/공변량 패턴에 대한 표준화 Pearson 잔차를 저장합니다. 외적 스튜던트화 Pearson 잔차를 우도 비율 Pearson 잔차라고도 합니다. Minitab은 외적 Pearson 잔차에 대해 Pregibon에서 설명하는 1단계 근사를 계산합니다.1 이 근사는 표준화 Pearson 잔차와 같습니다. 공식은 다음과 같습니다.

표기법

용어설명
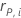i 번째 요인/공변량 패턴에 대한 Pearson 잔차
1, 이항 및 포아송 모형의 경우
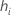i 번째 요인/공변량 패턴에 대한 레버리지

검증을 통한 표준화된 Pearson 잔차

검증 데이터의 경우 표준화된 Pearson 잔차에 대한 수식의 분모는 레버리지를 빼는 대신 레버리지를 추가합니다.

수식

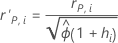
표기법

용어설명
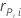
the Pearson residual for the i번째 validation row
1, for the binomial and Poisson models
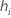the leverage for the i번째 validation row

이탈도 잔차

이탈도 잔차는 모형 이탈도에 기반을 두고 있으며, 적합하지 않은 요인/공변량 패턴을 식별하는 데 유용합니다. 모형 이탈도는 로그 우도 함수를 기반으로 하는 적합도 통계량입니다. i 번째 요인/공변량 패턴에 대해 정의되는 이탈도 잔차는 다음과 같습니다.

표기법

용어설명
yi i 번째 요인/공변량 패턴에 대한 반응 값
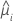i 번째 요인/공변량 패턴에 대한 적합치
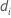i 번째 요인/공변량 패턴에 대한 이탈도

표준화 이탈도 잔차

표준화 이탈도 잔차는 특이치 식별에 도움이 됩니다. 공식은 다음과 같습니다.

표기법

용어설명
rD,ii 번째 요인/공변량 패턴에 대한 이탈도 잔차
hii 번째 요인/공변량 패턴에 대한 레버리지

검증을 통한 표준화된 이탈도 잔차

검증 데이터의 경우 표준화된 이탈도 잔차에 대한 수식의 분모는 레버리지를 빼는 대신 레버리지를 추가합니다.

수식

표기법

용어설명
rD,iThe deviance residual for the i번째 validation row
hiThe leverage for the i번째 validation row

외적 스튜던트화 이탈도 잔차

외적 이탈도 잔차는 데이터에서 i번째 사례를 제외함으로 인한 이탈도의 변동을 측정합니다. 외적 이탈도 잔차를 우도 비율 이탈도 잔차라고도 합니다. 외적 이탈도 잔차에 대해, Minitab은 Pregibon 1단계 근사 방법에 따라 1단계 근사를 계산합니다1. 공식은 다음과 같습니다.

표기법

용어설명
yii번째 요인/공변량 패턴의 반응 값
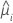i번째 요인 공변량 패턴에 대한 적합치
hii번째 요인/공변량 패턴의 레버리지
r'D,ii번째 요인/공변량 패턴에 대한 표준화 이탈도 잔차
r'P,ii번째 요인/공변량 패턴에 대한 표준화 Pearson 잔차

1. Pregibon, D. (1981). "Logistic Regression Diagnostics." The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.

델타 카이-제곱

Minitab에서는 j 번째 요인/공변량 패턴이 있는 모든 관측치를 삭제함으로써 발생하는 Pearson 카이-제곱의 변동을 계산합니다. 데이터의 각 구별 요인/공변량 패턴에 대해 델타 카이-제곱 값이 하나씩 저장됩니다. 델타 카이-제곱을 사용하여 적합하지 않은 요인/공변량 패턴을 탐지할 수 있습니다. 델타 카이-제곱의 공식은 다음과 같습니다.

공식

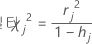
표기법

용어설명
hj 레버리지
rj Pearson 잔차

델타 이탈도

Minitab에서는 j 번째 요인/공변량 패턴이 있는 모든 관측치를 삭제하여 이탈도 통계량의 변동을 계산합니다. 데이터의 각 구별 요인/공변량 패턴에 대해 값이 하나씩 저장됩니다. 델타 이탈도를 사용하여 적합하지 않은 요인/공변량 패턴을 탐지할 수 있습니다. 이탈도 통계량의 변동은 다음과 같습니다.

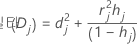
표기법

용어설명
hj레버리지
rjPearson 잔차
dj이탈도 잔차

델타 베타(표준화)

Minitab에서는 j 번째 요인/공변량 패턴이 있는 모든 관측치를 삭제하여 변동을 계산합니다. 데이터의 개별적인 각 요인/공변량 패턴에 대해 값이 하나씩 저장됩니다. 표준화 델타 β를 사용하여 계수 추정치에 큰 영향을 미치는 요인/공변량 패턴을 탐지할 수 있습니다. 이 값은 표준화 Pearson 잔차에 기초합니다.

공식

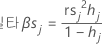
표기법

용어설명
hj 레버리지
rs j 표준화 Pearson 잔차

델타 베타

Minitab에서는 j 번째 요인/공변량 패턴이 있는 모든 관측치를 삭제하여 변동을 계산합니다. 데이터의 각 구별 요인/공변량 패턴에 대해 값이 하나씩 저장됩니다. 델타 β를 사용하여 계수 추정치에 큰 영향을 미치는 요인/공변량 패턴을 탐지할 수 있습니다. 이 값은 Pearson 잔차에 기초합니다.

공식

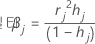
표기법

용어설명
hj 레버리지
rj Pearson 잔차

레버리지

레버리지는 일반화된 모자 행렬의 대각 요소들니다. 레버리지는 결과에 유의한 영향을 미칠 수 있는 요인/공변량 패턴을 탐지하는 데 유용합니다.

공식

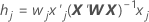
표기법

용어설명
wj 계수 적합의 가중 행렬의 j 번째 대각 요소
xj설계 행렬의 j 번째 행
X설계 행렬
X'X의 전치
W계수 추정의 가중 행렬

검증을 통한 레버리지

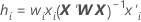
표기법

용어설명
wi the internal weight for the i번째 validation row
xithe row of the design matrix for the predictors in the i번째 validation row
Xthe design matrix for the training data set
X'the transpose of X
Wthe diagonal matrix of internal weights for the training data set

Cook의 거리

Minitab에서는 근사 Cook의 거리를 계산합니다.

공식

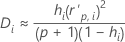
표기법

용어설명
hii 번째 요인/공변량 패턴의 레버리지
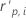i 번째 요인/공변량 패턴의 표준화된 Pearson 잔차
p회귀 자유도

DFITS

단일 외적 스튜던트화가 적합치에 미치는 영향의 측도. DFITS 값이 큰 관측치는 특이치일 수 있습니다. Minitab에서는 DFITS의 근사값을 계산합니다.

공식

표기법

용어설명
hi데이터 점의 레버리지
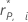데이터 점의 외적 스튜던트화 Pearson 잔차

분산 팽창 인수(VIF)

VIF를 계산하려면 나머지 예측 변수를 사용하여 가중 회귀 분석을 예측 변수에 대해 수행합니다. 가중 행렬은 계수 추정을 위해 McCullagh와 Nelder1에서 주어진 행렬입니다. 이 경우에 VIF 공식은 선형 회귀 공식과 동등합니다. 예를 들어 예측 변수가 xj인 경우 VIF 공식은 다음과 같습니다:

표기법

용어설명
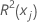반응 변수가 xj이고 예측 변수가 모형의 나머지 항인 결정 계수

1. P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2nd Edition, Chapman & Hall/CRC, London.

Copyright © 2024 Minitab, LLC. All rights Reserved.