지수 모임 및 연결 함수
기존 선형 모형을 일반화 선형 모형으로 확장하려면 지수 모임 분포와 연결 함수의 두 가지 부분이 필요합니다.
지수 모임
첫 부분에서는 선형 모형을 지수 모임이라는 큰 분포 모임의 구성원인 반응 변수로 확장합니다. 분포의 지수 모임에 속한 구성원은 관측된 반응에 대해 다음과 같은 일반적인 형식의 확률 분포 함수를 갖습니다.
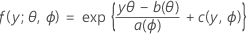
여기서 a(∙), b(∙) 및 c(∙)는 반응 변수의 분포에 따라 다릅니다. 모수 θ는 종종 정규 모수라고 하는 위치 모수이며, ϕ는 산포 모수라고 합니다. a(ϕ) 함수는 일반적으로 a(ϕ)= ϕ/ ω 형식이며, 여기서 ω는 알려진 상수이거나 관측치마다 다를 수 있는 가중치일 수 있습니다. (Minitab에서 가중치에 a(ϕ) 함수가 제공되면 적절하게 조정됩니다.)
지수 모임의 구성원은 이산형 분포이거나 계량형 분포일 수 있습니다. 지수 모임의 구성원인 계량형 분포의 예는 정규 및 감마 분포입니다. 지수 모임의 구성원인 이산형 분포의 예는 이항 및 포아송 분포입니다. 아래 표에는 이러한 분포 특성들이 나와 있습니다.
| 분포 | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| 정규 분포 | σ2 | θ2/2 | φω |  |
| 이항 분포 | 1 | 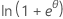 |
φ/ω | -ln(y!) |
| 포아송 분포 | 1 | exp(θ) | φ/ω |  |
연결 함수
두 번째 부분은 연결 함수입니다. 연결 함수는 i 번째 관측치의 반응 평균을 다음과 같은 형식으로 선형 예측 변수에 연결합니다.
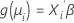
기존 선형 모형은 연결 함수가 항등원 함수인 이 일반 공식의 특별한 경우입니다.
두 번째 부분에서 선택하는 연결 함수는 첫 부분의 지수 모임의 특정 분포에 따라 결정됩니다. 특히 지수 모임의 각 분포에는 정규 연결 함수라는 특수 연결 함수가 있습니다. 이 연결 함수는 θ가 정규 모수인 g (μi) = Xi'β= θ 방정식을 충족합니다. 정규 연결 함수의 결과는 몇 가지 바람직한 모형의 통계적 속성입니다. 적합도 통계량은 다른 연결 함수를 사용하여 적합치를 비교하는 데 사용할 수 있습니다. 일부 연결 함수는 경험적인 이유로 또는 원칙에 있어 특별한 의미를 가지고 있기 때문에 사용할 수도 있습니다. 예를 들어, 로짓연결함수의 장점은 승산비의 추정치를 제공한다는 것입니다. 또 다른 예는 노밋 연결 함수에서는 이원 범주로 분류된 정규 분포를 따르는 기본 변수가 있다고 가정한다는 것입니다.
Minitab은 각 모형 등급에 대해 세 가지 연결 함수를 제공합니다. 서로 다른 연결 함수를 사용하여 다양한 데이터에 충분히 적합한 모형을 찾을 수 있습니다.
이항 분포 모형의 경우, 연결 함수는 로짓, 노밋(프로빗) 및 곰핏(보 로그-로그)입니다. 이 연결 함수들은 누적 로지스틱 분포 함수의 역함수(로짓), 표준 누적 정규 분포 함수의 역함수(노밋), 그리고 Gompertz 분포 함수의 역함수(곰핏)입니다. 로짓은 이항 분포 모형에 대한 정규 연결 함수이므로, 로짓이 기본 연결 함수입니다.
포아송 분포 모형의 경우 연결 함수는 자연 로그, 제곱근 및 항등원 함수입니다. 자연 로그는 포아송 분포 모형에 대한 정규 연결 함수이므로, 자연 로그가 기본 연결 함수입니다.
아래에는 연결 함수가 요약되어 있습니다.
| 모형 | 이름 | 연결 함수, g(μi) |
| 이항 분포 | 로짓 | 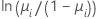 |
| 이항 분포 | 노밋(프로빗) | 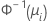 |
| 이항 분포 | 곰핏(보 로그-로그) |  |
| 포아송 분포 | 자연 로그 | 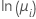 |
| 포아송 분포 | 제곱근 |  |
| 포아송 분포 | 항등원 | 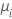 |
표기법
| 용어 | 설명 |
|---|---|
| μi | i 번째 행의 평균 반응 |
| g(μi) | 연결 함수 |
| X | 예측 변수의 벡터 |
| β | 예측 변수와 연관된 계수의 벡터 |
 | 정규 분포의 역 누적분포함수 |
계수
[1] P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2nd Ed., Chapman & Hall/CRC, London.
계수 표준 오차
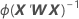
W는 대각 요소가 다음 공식에 의해 정해지는 대각 행렬입니다.
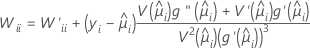
설명

이 분산-공분산 행렬은 Fisher의 정보 행렬이 아닌 관측된 Hessian 행렬에 기반을 두고 있습니다. Minitab에서는 관측된 Hessian 행렬을 사용하는데, 결과로 생성된 모형이 조건적 평균 오규격에 대해 더 로버스트하기 때문입니다.
정규 연결을 사용할 경우 관측된 Hessian 행렬과 Fisher의 정보 행렬은 동일합니다.
표기법
| 용어 | 설명 |
|---|---|
| yi | i 번째 행에 대한 반응 값 |
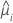 | i 번째 행에 대한 추정 평균 반응 |
| V(·) | 아래 표에 제공된 분산 함수 |
| g(·) | 연결 함수 |
| V '(·) | 분산 함수의 일차 도함수 |
| g'(·) | 연결 함수의 일차 도함수 |
| g''(·) | 연결 함수의 이차 도함수 |
분산 함수는 모형에 따라 다릅니다.
| 모형 | 분산 함수 |
| 이항 분포 | 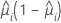 |
| 포아송 분포 | 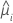 |
자세한 내용은 [1] 및 [2]에서 확인하십시오.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
이항 로지스틱 회귀 분석에 대한 승산비
승산비는 이항 반응이 포함된 모형에 대해 로짓 연결 함수를 선택하는 경우에만 제공됩니다. 이 경우 승산비는 예측 변수와 반응 간의 관계를 해석하는 데 있어 유용합니다.
승산비(τ)는 음수가 아닌 숫자입니다. 승산비 = 1은 비교 기준으로 사용됩니다. τ = 1이면 반응과 예측 변수 간에 연관성이 없습니다. τ < 1이면 요인의 기준 수준(또는 계량형 예측 변수)에 대한 사건의 확률이 더 높습니다. τ > 1이면 요인의 기준 수준(또는 계량형 예측 변수)에 대한 사건의 확률이 더 작습니다. 값이 1에서 멀리 떨어질수록 더 강한 연관도를 나타냅니다.
참고
공변량 또는 요인이 1개인 이항 로지스틱 회귀 모형의 경우 추정된 승산비는 다음과 같습니다.
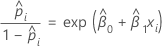
지수 관계는 β에 대한 해석을 제공합니다. x가 한 단위 증가할 때마다 확률이 eβ1씩 증가합니다. 승산비는 exp(β1)와 같습니다.
예를 들어, β가 0.75인 경우 승산비는 exp(0.75) = 2.11입니다. 이는 x가 한 단위 증가할 때마다 승산비가 111% 증가한다는 것을 나타냅니다.
표기법
| 용어 | 설명 |
|---|---|
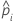 | 데이터의 i번째 행에 대해 추정된 성공 확률 |
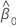 | 추정된 절편 계수 |
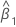 | 예측 변수 x에 대해 추정된 계수 |
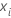 | i번째 행에 대한 데이터 점 |
분산-공분산 행렬
d가 예측 변수의 수 더하기 1인 d x d 행렬. 각 계수의 분산은 대각 셀에 있고 각 계수 쌍의 공분산은 해당 대각 외 셀에 있습니다. 분산은 계수 제곱의 표준 오차입니다.
분산-공분산 행렬은 정보 행렬의 역행렬의 마지막 반복에서 나옵니다. 분산-공분산 행렬의 형식은 다음과 같습니다.
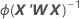
W는 대각 요소가 다음 공식에 의해 정해지는 대각 행렬입니다.

설명

이 분산-공분산 행렬은 Fisher의 정보 행렬이 아닌 관측된 Hessian 행렬에 기반을 두고 있습니다. Minitab에서는 관측된 Hessian 행렬을 사용하는데, 결과로 생성된 모형이 조건적 평균 오규격에 대해 더 로버스트하기 때문입니다.
정규 연결을 사용할 경우 관측된 Hessian 행렬과 Fisher의 정보 행렬은 동일합니다.
표기법
| 용어 | 설명 |
|---|---|
| yi | i 번째 행에 대한 반응 값 |
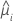 | i 번째 행에 대한 추정 평균 반응 |
| V(·) | 아래 표에 제공된 분산 함수 |
| g(·) | 연결 함수 |
| V '(·) | 분산 함수의 일차 도함수 |
| g'(·) | 연결 함수의 일차 도함수 |
| g''(·) | 연결 함수의 이차 도함수 |
분산 함수는 모형에 따라 다릅니다.
| 모형 | 분산 함수 |
| 이항 분포 | 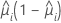 |
| 포아송 분포 | 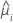 |
자세한 내용은 [1] 및 [2]에서 확인하십시오.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
