한 의료 연구자가 새 약품의 투여량 수준이 성인의 박테리아 존재에 어떤 영향을 미치는지 확인하려고 합니다. 연구자는 환자 30명과 6개의 투여량 수준을 사용하여 실험을 수행합니다. 2주 동안, 연구자는 환자 5명에게 한 가지 투여량 수준을 제공하고, 다른 환자 5명에게 다른 투여량 수준을 제공하고, 이런 식으로 계속합니다. 2주가 지나면 각 환자를 검사하여 박테리아가 발견되는지 여부를 확인합니다.
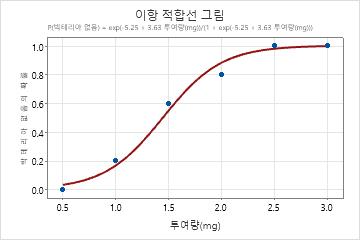
데이터에 이항 반응과 하나의 연속형 예측 변수가 포함되어 있기 때문에 연구자는 약품의 투여량이 박테리아의 존재와 관계가 있는지 여부를 확인하기 위해 이항 적합선 그림을 사용합니다.
- 표본 데이터를 엽니다 박테리아약품.MWX.
- 을 선택합니다.
- 드롭다운 리스트에서 사건/시행 형식의 반응을 선택합니다.
- 사건 이름에 박테리아 없음을 입력합니다.
- 사건 발생 횟수에 '박테리아 없음'을 입력합니다.
- 시행 횟수에 시행을 입력합니다.
- 예측 변수에 '투여량(mg)'을 입력합니다.
- 그래프을(를) 클릭합니다. 잔차 그림 아래에서 네 개 모두을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
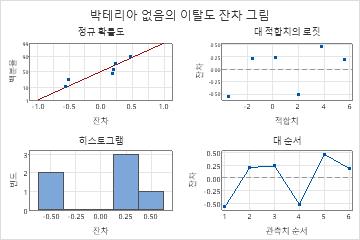
약물 복용량에 대한 p-값은 유의 수준 0.05보다 작습니다. 이 결과는 약물 복용량과 박테이라의 존재 간의 관계가 통계적으로 유의하다는 것을 나타냅니다. 이항 적합선 그림은 복용량이 증가하면 박테리아가 존재하지 않을 확률이 증가한다는 것을 보여줍니다. 게다가 승산비는 복용량 수준이 1mg 증가할 때마다 박테리아가 존재하지 않을 확률이 약 38배 증가한다는 것을 나타냅니다. 적합선 그림은 모형이 데이터를 잘 적합시킨다는 것을 보여주며 잔차 그림은 모형에 문제가 없음을 나타냅니다.
방법
| 연결 함수 | 로짓 |
|---|---|
| 사용된 행 | 6 |
반응 정보
| 변수 | 값 | 카운트 | 사건 이름 |
|---|---|---|---|
| 박테리아 없음 | 사건 | 18 | 박테리아 없음 |
| 비사건 | 12 | ||
| 시행 | 총계 | 30 |
회귀 방정식
| P(박테리아 없음) = exp(-5.25 + 3.63 투여량(mg))/(1 + exp(-5.25 + 3.63 투여량(mg))) |
|---|
계수
| 항 | 계수 | SE 계수 | VIF |
|---|---|---|---|
| 상수 | -5.25 | 1.99 | |
| 투여량(mg) | 3.63 | 1.30 | 1.00 |
계량형 예측 변수에 대한 승산비
| 승산비 | 95% CI | |
|---|---|---|
| 투여량(mg) | 37.5511 | (2.9647, 475.6190) |
모형 요약
| 이탈도 R-Sq | 이탈도 R-Sq(수정) | AIC | AICc | BIC |
|---|---|---|---|---|
| 96.04% | 91.81% | 10.63 | 14.63 | 10.22 |
분산 분석
| 출처 | DF | 수정 분산 | 수정 평균 | 카이-제곱 | P-값 |
|---|---|---|---|---|---|
| 회귀 | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 투여량(mg) | 1 | 22.7052 | 22.7052 | 22.71 | 0.000 |
| 오차 | 4 | 0.9373 | 0.2343 | ||
| 총계 | 5 | 23.6425 |