참고
이 명령은 예측 분석 모듈에서 사용할 수 있습니다. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
TreeNet® 모형은 단일 분류 또는 회귀 트리보다 더 정확하고 과도 적합에 대한 내성이 더 높은 분류 및 회귀 분석 문제를 해결하기 위한 접근 방식입니다. 공정에 대한 광범위하고 일반적인 설명은 작은 회귀 트리를 초기 모형으로 시작한다는 것입니다. 해당 트리에서 다음 회귀 트리에 대한 반응 변수가 되는 데이터의 모든 행에 대한 잔차가 옵니다. 다른 작은 회귀 트리를 만들어 첫 번째 트리 잔차를 예측하고 결과 잔차를 다시 계산합니다. 최소 예측 오차가 있는 최적의 트리 수가 검증 방법을 사용하여 식별될 때까지 이 순서를 반복합니다. 결과 트리 순서는 TreeNet® 회귀 모형을 만듭니다.
회귀 사례의 경우 분석에 대한 일반적인 설명을 추가할 수 있지만 일부 세부 사항은 다음의 손실 함수에 따라 다릅니다.
| 통계량 | 값 |
|---|---|
초기 적합치,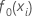 
|
반응 변수의 평균 |
일반화 잔차,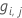 
행
i에 대한 응답 값으로
|
|
노드 업데이트 내에서, 
|
의 평균
|
| 통계량 | 값 |
|---|---|
초기 적합치,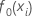 
|
반응 변수의 중위수 |
일반화 잔차,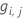 
행
i에 대한 응답 값으로
|
|
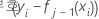
노드 업데이트 내에서, 
|
의 중위수 
|
Huber 손실 기능
Huber 손실 함수의 경우 통계는 다음과 같습니다.
초기 적합치,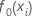 
모든
응답 값의 중위수 같습니다.
jth 트리를 성장시키기 위해,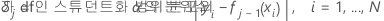 
그런 다음 i 행에 대한 일반화된 잔차는 다음과 같습니다.
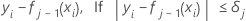
일반화된 잔차는 j 트리를 성장시키는 반응 값으로 사용됩니다.
j 트리의 m번째 단말 노드의 행에 대한 업데이트된 값은 다음과 같습니다.
j-1
트리가 성장한 후
i번째 행의 정규 잔차가 될 수 있습니다. 그러면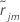 
의
중위수가 됨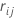 
j번째
트리의 단말 노드
m 내부의 행값입니다. 그런 다음
j번째 트리의
m번째 단말 노드 내부의 모든 행에 대해 업데이트된 값은 다음과 같습니다. 
이전 식의 평균은 j 트리의 단말 노드 m 내부의 모든 행에 걸쳐 계산됩니다.
손실 함수에 대한 표기법
앞의 세부 정보에서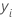 
은(는)
행
i에 대한 반응 변수의 값, 
은(는)
이전
j – 1 트리의 적합치, 그리고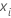 
는
학습 데이터에서 예측 변수 값의
i번째 행을 나타내는 벡터입니다.
입력 매개 변수
| 입력 | 기호 |
|---|---|
| 학습 속도 |  |
| 표본 비율 |  |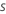
| 트리당 최대 단말 노드 수 |  |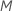
| 트리 수 |  |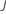
| 전환 값 |  |
일반 프로세스
- 학습 데이터에서 크기 s * N의 임의 표본을 그립니다. 여기에서 N은 학습 데이터의 행 수입니다.
- 일반화 잔차 를 계산합니다.
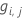,에
대한 
.
- 최대 M개 단말 노드가 있는 회귀 트리를 일반화 잔차에 적합합니다. 트리는 관측치를 최대 M개의 상호 배타적 그룹으로 분할합니다.
- 회귀 트리의
m번째 단말 노드의 경우 손실 함수에 의존하는 트리에 대한 노드 내 업데이트를 계산하고,
.
- 학습률에 따라 노드 내 업데이트를 축소하고 값을
적용하여 업데이트된 적합치, 를 가져옵니다.
:
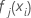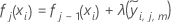
- 분석에서 각 J의 트리에 대해 1~5단계를 반복합니다.
