참고
이 명령은 에서 사용할 수 있습니다예측 분석 모듈. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
연구원 팀은 대출자에 대한 데이터와 부동산 위치에 대한 데이터를 사용하여 모기지 금액을 예측하려고 합니다. 변수에는 대출자의 소득, 인종 및 성별뿐만 아니라 재산의 인구조사 지역 위치 및 대출자 및 자산 유형에 대한 기타 정보가 포함됩니다.
중요한 예측 변수를 식별하기 위한 초기 탐색 CART® 회귀 분석 후 팀은 이제 필요한 후속 단계로 간주 TreeNet® 회귀 분석 합니다. 연구원은 반응과 중요한 예측 변수 사이의 관계를 더 많이 이해하고 새로운 관측치에 대한 확률을 더 정확하게 예측하기를 희망합니다.
이러한 데이터는 연방 주택 대출 은행 모기지에 대한 정보가 포함된 공개 데이터 집합을 기준으로 조정되었습니다. 원본 데이터는 fhfa.gov에서 나온 것입니다.
- 표본 데이터 세트를 엽니다 구입모기지.MTW.
- 을 선택합니다.
- 반응에 대출 금액를 입력합니다.
- 계량형 예측 변수에 연간 소득 – 지역 소득 를 입력합니다.
- 범주형 예측 변수에 첫 주택 구매자 – 대도시 중심 지역 를 입력합니다.
- 검증을 클릭합니다.
- 검증 방법에서 K-접기 교차 검증를 선택합니다.
- 접기 수(K)에 3을 입력합니다.
- 각 대화 상자에서 확인를 클릭합니다.
결과 해석
이 분석을 위해 Minitab은 300개의 트리를 키우고 최적의 트리 수는 300개입니다. 최적의 트리 수가 모형이 키우는 최대 트리 수에 근접해지기 때문에 연구원들은 더 많은 트리로 분석을 반복합니다.
모형 요약
| 전체 예측 변수 | 34 |
|---|---|
| 중요 예측 변수 | 19 |
| 성장한 트리 수 | 300 |
| 최적의 트리 수 | 300 |
| 통계량 | 교육 | 검정 |
|---|---|---|
| R-제곱 | 94.02% | 84.97% |
| 루트 평균 제곱 오차(RMSE) | 32334.5587 | 51227.9431 |
| 평균 제곱 오차(MSE) | 1.04552E+09 | 2.62430E+09 |
| 평균 절대 편차(MAD) | 22740.1020 | 35974.9695 |
| 평균 절대 백분율 오차(MAPE) | 0.1238 | 0.1969 |
500개의 트리가 있는 예
- 결과에서 하이퍼파라미터 튜닝 를 선택합니다.
- 트리 수에 500를 입력합니다.
- 결과 표시을 클릭합니다.
결과 해석
이 분석을 위해 500개의 트리가 성장되었고, 하이퍼파라미터의 조합에 대한 최적의 트리 수가 정확도 기준의 최고값인 500입니다. 하위 표본 부분은 원래 분석에서 0.5대신 0.7로 변경됩니다. 학습률은 원래 분석에서 0.04372가 아닌 0.0437로 변경됩니다.
모형 요약 표과 R-제곱 대 트리 수 그림을 모두 검사합니다. 트리 수가 500개일 때의R2 값은 검정 데이터의 경우 86.79%이고 훈련 데이터의 경우 96.41%입니다. 이러한 결과는 기존 회귀 분석 및 에 비해 개선되었음을 CART® 회귀 분석보여줍니다.
방법
| 손실 함수 | 제곱 오차 |
|---|---|
| 최적 트리 수 선택 기준 | 최대 R-제곱 |
| 모형 검증 | 3-접기 교차 검증 |
| 학습률 | 0.04372 |
| 하위 표본 부분 | 0.5 |
| 트리당 최대 터미널 노드 수 | 6 |
| 최소 단말 노드 크기 | 3 |
| 노드 분할을 위해 선택된 예측 변수 수 | 총 예측 변수 수 = 34 |
| 사용된 행 | 4372 |
반응 정보
| 평균 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
방법
| 손실 함수 | 제곱 오차 |
|---|---|
| 최적 트리 수 선택 기준 | 최대 R-제곱 |
| 모형 검증 | 3-접기 교차 검증 |
| 학습률 | 0.001, 0.0437, 0.1 |
| 하위 표본 부분 | 0.5, 0.7 |
| 트리당 최대 터미널 노드 수 | 6 |
| 최소 단말 노드 크기 | 3 |
| 노드 분할을 위해 선택된 예측 변수 수 | 총 예측 변수 수 = 34 |
| 사용된 행 | 4372 |
반응 정보
| 평균 | 표준 편차 | 최소값 | Q1 | 중위수 | Q3 | 최대값 |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
하이퍼파라미터 최적화
| 모형 | 최적의 트리 수 | R-제곱(%) | 평균 절대 편차 | 학습률 | 하위 표본 부분 | 최대 단말 노드 |
|---|---|---|---|---|---|---|
| 1 | 500 | 36.43 | 82617.1 | 0.0010 | 0.5 | 6 |
| 2 | 495 | 85.87 | 34560.5 | 0.0437 | 0.5 | 6 |
| 3 | 495 | 85.63 | 34889.3 | 0.1000 | 0.5 | 6 |
| 4 | 500 | 36.86 | 82145.0 | 0.0010 | 0.7 | 6 |
| 5* | 500 | 86.79 | 33052.6 | 0.0437 | 0.7 | 6 |
| 6 | 451 | 86.67 | 33262.3 | 0.1000 | 0.7 | 6 |
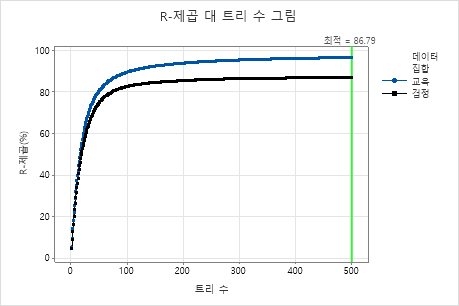
모형 요약
| 전체 예측 변수 | 34 |
|---|---|
| 중요 예측 변수 | 24 |
| 성장한 트리 수 | 500 |
| 최적의 트리 수 | 500 |
| 통계량 | 교육 | 검정 |
|---|---|---|
| R-제곱 | 96.41% | 86.79% |
| 루트 평균 제곱 오차(RMSE) | 25035.7243 | 48029.9503 |
| 평균 제곱 오차(MSE) | 6.26787E+08 | 2.30688E+09 |
| 평균 절대 편차(MAD) | 17309.3936 | 33052.6087 |
| 평균 절대 백분율 오차(MAPE) | 0.0930 | 0.1790 |
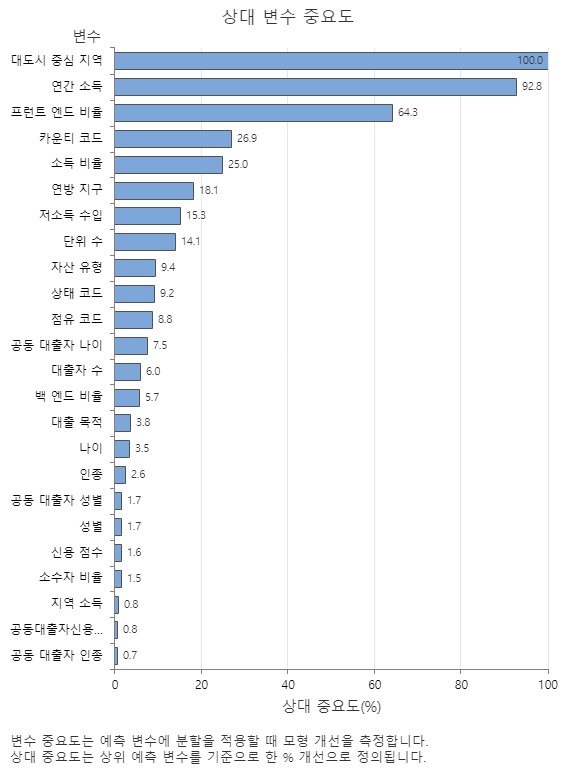
상대 변수 중요도 그래프는 트리 시퀀스에 대한 예측 변수에 분할이 이루어질 때 모형 개선에 미치는 영향 순으로 예측 변수를 표시합니다. 가장 중요한 예측 변수는 대도시 중심 지역입니다. 상위 예측 변수인 Core Based Statistical Area의 중요도가 100%인 경우 다음 중요 변수인 연간 소득의 기여도는 92.8%입니다. 이는 차용인의 연간 소득이 부동산의 지리적 위치만큼 92.8 % 중요하다는 것을 의미합니다.
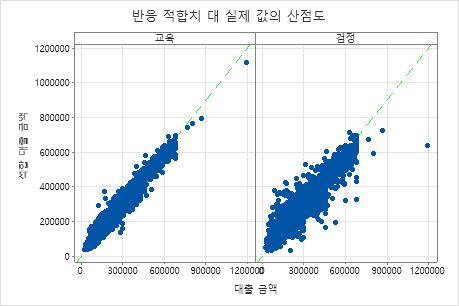
적합된 대출 금액 대 실제 대출 금액의 산점도는 학습 데이터와 검정 데이터 모두에 대한 적합치와 실제 값 간의 관계를 보여줍니다. 그래프의 점 위로 마우스를 가져가 표시된 값을 보다 쉽게 볼 수 있습니다. 이 예제에서는 모든 점이 거의 y=x 기준선 근처에 있습니다.
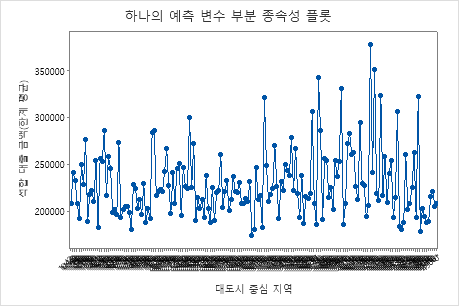
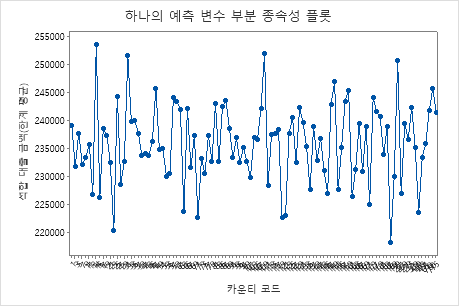
부분 종속성도를 사용하면 중요한 변수 또는 변수 쌍이 적합 반응 값에 어떤 영향을 미치는지 파악할 수 있습니다. 부분 종속성 플롯은 반응과 변수 간의 관계가 선형, 단조로움 또는 더 복잡한지 여부를 보여줍니다.
첫 번째 그림은 각 코어 기반 통계 영역에 대한 적합된 대출 금액을 보여줍니다. 데이터 점이 너무 많기 때문에 개별 데이터 점 위로 마우스를 가져가 특정 x-값 및 y-값을 볼 수 있습니다. 예를 들어 그래프의 오른쪽에 있는 가장 높은 점은 코어 영역 번호 41860이고 적합된 대출 금액은 약 $378069입니다.
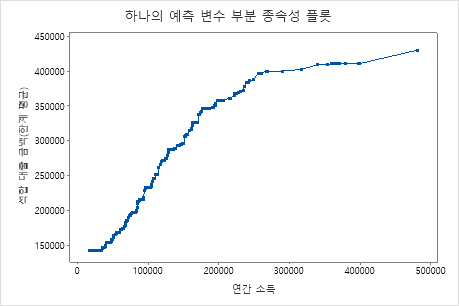
두 번째 그림은 연간 소득이 증가함에 따라 적합된 대출 금액이 증가한다는 것을 보여줍니다. 연간 소득이 $300000에 도달하면 적합 대출 금액 수준이 더 느린 속도로 증가합니다.
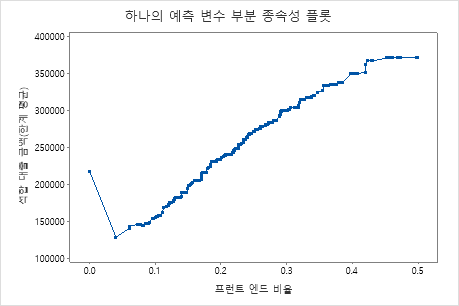
세 번째 그림은 프런트 엔드 비율이 증가함에 따라 적합된 대출 금액이 증가한다는 것을 보여줍니다.
네 번째 그림은 각 인구 조사 카운티 코드에 대한 적합된 대출 금액을 보여줍니다. 첫 번째 그림과 마찬가지로 특정 데이터 점 위로 마우스를 가져가 더 많은 정보를 얻을 수 있습니다. 다른 변수에 대한 도표를 생성하려면 또는 를 선택합니다
