참고
이 명령은 예측 분석 모듈에서 사용할 수 있습니다. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
중요한 변수
Minitab Statistical Software는 변수의 중요성을 평가하는 두 가지 방법을 제공합니다.
순열
- A = 87
- B = 9
- C = 4
그런 다음 해당 행의 마진은 0.87 - 0.09 = 0.78입니다.
평균 OOB 마진은 모든 데이터 행의 평균 마진입니다.
변수의 중요성을 확인하려면 OOB 데이터를 통해 변수의 값 xm을 임의로 순열합니다. 응답 값과 다른 예측 변수 값을 동일하게 둡니다. 그런 다음 동일한 단계를 사용하여 순열된 데이터,  의 평균 마진을 계산합니다.
의 평균 마진을 계산합니다.
변수 xm의 중요성은 두 평균의 차이에서 비롯됩니다.
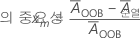
설명  은(는) 순열 전의 평균 마진입니다. Minitab은 10–7보다 작은 값을 0으로 반올림합니다.
은(는) 순열 전의 평균 마진입니다. Minitab은 10–7보다 작은 값을 0으로 반올림합니다.
지니
모든 분류 트리는 분할의 컬렉션입니다. 각 분할은 트리를 개선합니다.
다음 수식은 단일 노드에서 개선된 기능을 제공합니다.
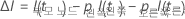
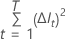
설명  는 분할된 노드 수이며
는 분할된 노드 수이며  모든 노드에 대해
모든 노드에 대해  관심 변수가 스플리터가 아닙니다.
관심 변수가 스플리터가 아닙니다.
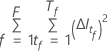
설명 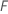 는 포리스트에서 트리의 수이며
는 포리스트에서 트리의 수이며 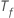 는 트리
는 트리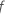 에서 분할되는 노드 수입니다.
에서 분할되는 노드 수입니다.
노드 불순도의 계산은 지니 방법과 유사합니다. 지니 방법에 대한 자세한 내용은 노드 분할 방법 CART® 분류로 이동하십시오.
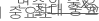
평균 로그 우도
OOB 데이터
계산은 포리스트의 모든 트리의 OOB 표본을 사용합니다. OOB 표본의 특성상 다양한 트리 조합을 사용하여 데이터의 각 행에 대한 로그 우도에 대한 기여를 찾을 수 있습니다.
포리스트에 있는 지정된 트리의 경우, OOB 데이터의 행에 대한 클래스 투표는 단일 트리의 행에 대한 예측 클래스입니다. OOB 데이터에서 열에 대한 예측 클래스는 포리스트의 모든 트리에서 가장 높은 투표를 가진 클래스입니다. OOB 데이터에서 행에 대한 예측 클래스 확률은 클래스의 투표 수와 행의 총 투표 비율입니다. 공산 계산은 다음과 같은 확률에서 따릅니다.
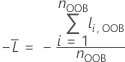
설명

및 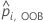 는 OOB 데이터에서 행 i에 대한 계산된 사건 확률입니다.
는 OOB 데이터에서 행 i에 대한 계산된 사건 확률입니다.
OOB 데이터 표기법
| 용어 | 설명 |
|---|---|
| nOOB | 하나 이상의 OOB인 행 수 |
| yi,OOB | OOB 데이터에서 사례의 이항 반응 값 i. yi, OOB = 사건 클래스의 경우 1, 그렇지 않으면 0. |
검정 집합
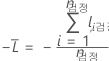
포리스트에 지정된 트리의 경우 검정 집합의 행에 대한 클래스 투표는 단일 트리의 행에 대한 예측 클래스입니다. 검정 집합의 행에 대한 예측 클래스는 포리스트의 모든 트리에서 가장 높은 투표를 가진 클래스입니다. 검정 집합에서 행에 대한 예측 클래스 확률은 클래스의 투표 수와 행의 총 투표 비율입니다. 공산 계산은 다음과 같은 확률에서 따릅니다.
설명
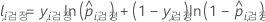
검정 집합 표기법
| 용어 | 설명 |
|---|---|
| nTest | 검정 집합의 표본 크기 |
| yi, Test | 검정 집합에서 사례의 이항 반응값 i. yi, k = 사건 클래스의 경우 1, 그렇지 않으면 0. |
 | 검정 집합에서 사례의 예측 사건 확률 i |
ROC 곡선 아래의 면적
수식


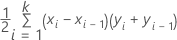
여기서 k는 고유한 사건 확률의 수이고 (x0, y0)은 점(0, 0)입니다.
OOB 데이터 또는 검정 집합에서 곡선에 대한 면적을 계산하려면 해당 곡선의 점을 사용합니다.
표기법
| 용어 | 설명 |
|---|---|
| TPR | 진양성률 |
| FPR | 가양성률 |
| TP | 진양성, 올바르게 평가된 사건 |
| FN | 가음성, 잘못 평가된 사건 |
| P | 실제 긍정적인 사건의 수 |
| FP | 가음성, 잘못 평가된 비사건 |
| N | 실제 부정적인 사건 수 |
| FNR | 가음성률 |
| TNR | 진음성률 |
예제
| x(가양성률) | y(진양성률) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
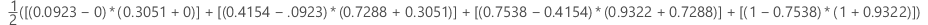

ROC 곡선 아래 면적에 대한 95% CI
다음 간격은 신뢰 구간에 대한 상한 및 하한을 제공합니다.
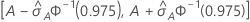
ROC 곡선 아래 면적의 표준 오차 계산(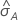 )은 Salford Predictive Modeler®에서 제공됩니다. ROC 곡선 아래의 면적 분산 추정에 대한 일반적인 정보는 다음 참조 자료를 참고하십시오.
)은 Salford Predictive Modeler®에서 제공됩니다. ROC 곡선 아래의 면적 분산 추정에 대한 일반적인 정보는 다음 참조 자료를 참고하십시오.
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., & Baumgartner, R. (2017). 작은 표본 크기의 연속 진단 검정을 위해 ROC 곡선 아래의 면적에 대한 신뢰도/신뢰할 수 있는 구간 방법의 비교입니다. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
표기법
| 용어 | 설명 |
|---|---|
| A | ROC 곡선 아래 면적 |
 | 표준 정규 분포의 0.975 백분위수 |
향상도
누적 향상도에 대한 일반적인 계산은 Random Forests® 분류의 누적 향상도 차트에 대한 방법 및 공식에서 확인하십시오.
오분류 비율
다음 방정식은 오분류 비율을 제공합니다.

오분류 카운트는 예측 클래스가 실제 클래스와 다른 OOB 데이터의 행 수입니다. 총 카운트는 OOB 데이터의 총 행 수입니다.
검정 데이터 집합을 사용한 검증 오분류된 카운트는 검정 집합의 오분류 합계입니다. 전체 카운트는 검정 데이터 집합의 행 수입니다.
