참고
이 명령은 예측 분석 모듈에서 사용할 수 있습니다. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
MARS® 회귀 분석 기본적으로 조각별 선형 회귀를 피팅하여 유연한 모델을 구축합니다. 모델에는 조각별 선의 끝점이 균등하게 결합된다는 제한이 있습니다. 모형의 비선형성에 대한 근사는 데이터의 고유한 구간에서 별도의 회귀 기울기를 사용합니다. 프로세스의 근사치는 간단한 2차원 사례에서 쉽게 시각화할 수 있습니다.
2차원의 경우 단일 직선이 데이터에 적합합니다. 이 모델은 복잡성 추가의 개선을 테스트하기 위한 기준을 제공합니다.
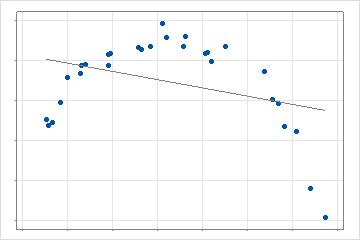
다음 단계에서 분석은 검색 기준에서 가장 큰 개선을 가져오는 기저 함수를 생성하는 예측 변수의 값을 검색합니다. 기준의 계산은 분석 선택 및 검증 방법에 따라 다릅니다. 2차원의 경우 이 모델은 1개 라인 대신 2개 라인이 있는 조각별 선형 회귀입니다. 예측 변수가 여러 개인 경우 최상의 데이터 점을 검색하면 분석에서 허용하는 각 예측 변수가 평가됩니다.
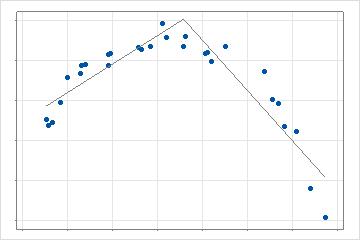
분석에서 최상의 개선을 제공하는 첫 번째 값을 찾은 후 나머지 예측 변수 값을 검색하여 현재 모형에 대한 최상의 개선을 찾습니다. 2차원의 경우 이 모델에는 데이터의 다른 부분을 설명하는 3개의 선이 있습니다. 검색은 분석에 대한 최대 기저 함수 수까지 반복됩니다. 교호작용이 허용되면 분석은 후보 기저 함수에 모형에 이미 있는 다른 기저 함수를 곱하여 추가 일련의 검색을 수행합니다.
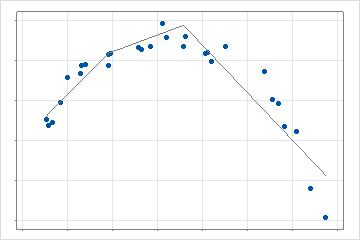
분석이 최대 기저 함수 개수를 빠르게 적합시키고 해당 함수의 모수를 추정한 후 분석에서 최적의 기저 함수 개수를 식별합니다. 최적 기저 함수 개수는 단계적 역방향 제거 접근 방식을 사용하여 최적성 기준의 최적 값을 가진 기저 함수의 개수를 찾습니다.
모형 적합치에 대한 결측값
기저 함수 검색에서 결 MARS® 회귀 분석 측값이 있는 예측 변수에 대한 지표 변수를 만듭니다. 인디케이터 변수는 예측 변수의 값이 누락되었는지 여부를 보여줍니다. 분석에 모형에 결측값이 있는 예측 변수에 대한 기저 함수가 포함된 경우 모형에는 지표 변수에 대한 기저 함수도 포함됩니다. 예측 변수에 대한 다른 기저 함수는 모두 지표 변수에 대한 기저 함수와 상호 작용합니다.
예측 변수에 결측값이 있는 경우 인디케이터 변수의 기저 함수는 0을 곱하여 해당 예측 변수에 대한 다른 기저 함수를 무효화합니다. 결측값에 대한 이러한 기본 함수는 중요한 예측 변수에 결측값이 있는 모든 모형, 심지어 추가 모형과 다른 유형의 변환을 비활성화하는 모형에도 있습니다.
예측에 대한 결측값
MARS® 회귀 분석 모형의 예측 변수에 결측값이 있는 경우 예측을 계산합니다. 분석에서는 분석이 모형을 적합할 때 예측 변수에 대한 결측값이 존재했는지 여부에 따라 다른 전략을 사용합니다. 분석이 모형을 적합할 때 예측 변수에 대한 결측값이 있는 경우 모형의 기저 함수에는 예측 변수에 결측값이 있을 때 모형에서 예측 변수를 제거하는 지표 변수가 포함됩니다.
두 번째 경우는 예측 변수에 대한 결측값이 예측값에 포함되지만 분석이 모형을 적합할 때 예측 변수에 결측값이 없는 경우입니다. 이 경우 예측을 계산하기 위해 분석은 결측값을 대체합니다. 계량형 예측 변수의 경우 예측 변수의 평균이 결측값을 대체합니다. 범주형 예측 변수의 경우 데이터 집합의 최종 비결측값이 결측값을 대체합니다.
