참고
이 명령은 예측 분석 모듈에서 사용할 수 있습니다. 모듈을 활성화하는 방법에 대한 자세한 내용은 여기를 클릭하십시오.
y = b0 + b1BF1 + b2BF2 + ... + bkBFk
- y는 반응 변수입니다.
- b0 은 상수항입니다.
- b1 + b2 + ... + bk 는 기저 함수에 대한 계수입니다.
- BF1 + BF2 + ... + BFk 는 기본 함수입니다.
예측 변수의 값에 대한 기저 함수를 풀어 반응의 예측 값을 계산합니다.
기본 기능
- 최대(0, X − c)
- 양의 계수
- 기여도는 c까지 0이며 증가합니다.
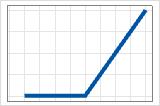
- 최대(0, X − c)
- 음의 계수
- 기여도는 c까지 최대값이며 감소한다.
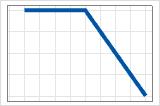
- 최대(0, c − X)
- 양의 계수
- 기여도는 최대값에서 시작하여 c까지 감소합니다. c 이후에는 기여도가 0입니다.
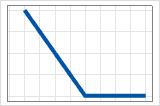
- 최대(0, c − X)
- 음의 계수
- 기여도는 0에서 시작하여 c까지 증가합니다. c 이후에는 기여도가 최대값입니다.
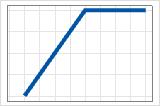
c가 예측 변수의 최소값 또는 최대값과 같으면 예측 변수는 기저 함수의 모든 값에 대해 동일한 효과를 갖습니다. 이 2개의 경우에 대한 부분 종속성도는 직선을 보여줍니다. MARS® 회귀 분석 c를 예측 변수에 대한 변환을 허용하지 않는 분석의 끝점 중 하나로 만듭니다.
범주형 예측 변수의 경우 기저 함수는 지표 함수입니다. 함수의 값은 일부 범주의 경우 0이고 다른 범주의 경우 값은 1입니다. 기본 함수의 형식은 다음과 같습니다.
X가 x1일 때 ... Xk 여기서 k 는 기저 함수의 수준 수이고k ≥ 1입니다.
함수의 값은 기저 함수의 범주에 대해 1입니다. 회귀 방정식의 계수에 대한 기저 함수의 곱셈은 함수가 0에서 1로 변경 될 때의 효과를 결정합니다.
1 기저 함수에서 계량형 예측 변수의 예
이 결과에서 BF2는 회귀 방정식에서 음의 계수를 갖습니다. 기저 함수에 대한 계수는 −57.6167입니다. 기저 함수의 배열은 max(0, c − X)입니다. 이 배열에서는 예측 변수가 증가하면 기저 함수의 값이 감소합니다. 이 배열과 음수 계수의 조합은 예측 변수와 반응 변수 사이에 양의 관계를 생성합니다. 이 거실 공간 지역의 효과는 438에서 3,078로 증가하는 판매 가격 것입니다. 의 거실 공간 기울기는 438에서 3,078까지 57.6167입니다.
회귀 방정식
BF3 = 품질이(가) 8, 9, 10인 경우
BF6 = 최대(0, 2002 - 준공)
BF7 = 지하 1층이(가) 누락되지 않은 경우
BF10 = 최대(0, 1696 - 지하 1층) * BF7
BF11 = 품질이(가) 1, 8인 경우
BF13 = 유형이(가) 90, 150, 160, 180, 190인 경우
BF15 = 이웃이(가) 블루스템, 클리어 크릭, 크로포드, 그린 힐스, 랜드마크, 노스리지, 노스리지 하이츠, 서머셋 빌리지, 스톤 브리지, 팀버랜드, 비엔커인 경우
BF17 = 지하 총면적이(가) 누락되지 않은 경우
BF19 = 최대(0, 지하 총면적 - 1392) * BF17
BF21 = 최대(0, 1층 공간 - 2402)
BF23 = 상태이(가) 1, 2, 3, 4, 5, 6인 경우
BF25 = 품질이(가) 1, 7, 10인 경우
BF27 = 최대(0, 1층 공간 - 2207)
BF30 = 최대(0, 15138 - 로트 지역)
판매 가격 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
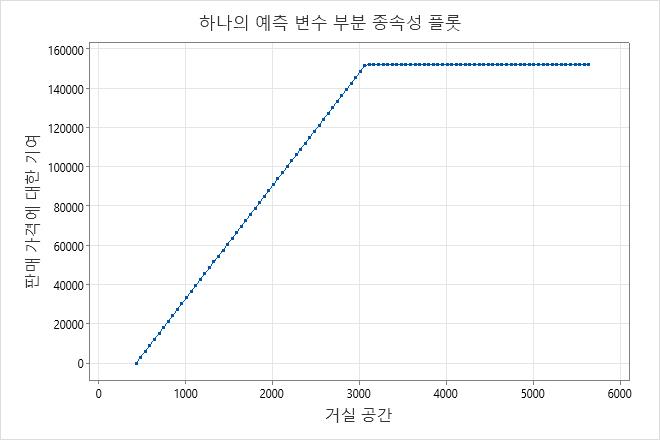
하나의 예측 변수 부분 종속성 그림
가산 모형에서는 단일 예측 변수, 부분 종속성 그림을 사용하여 중요한 계량형 예측 변수가 예측 반응에 어떤 영향을 미치는지 파악할 수 있습니다. 하나의 예측 변수 부분 종속성 플롯은 예측 변수 수준이 변경됨에 따라 반응이 어떻게 변경되는지 나타냅니다. 의 경우 그림의 MARS® 회귀 분석값은 x축의 예측 변수에 대한 기저 함수에서 가져옵니다. y축의 기여도는 그림의 최소값이 0이 되도록 표준화됩니다.
이 플롯은 데이터 세트의 최소 평방 피트에서 약 3,000 평방 피트로 증가함에 따라 거실 공간 증가한다는 것을 판매 가격 보여줍니다. 거실 공간 3,000평방피트에 도달하면 기부금 판매 가격 은 약 $152,000로 평평해집니다.
1 기저 함수에서 범주형 예측 변수의 예
이 결과에서 BF3은 예측 변수에 품질대한 것입니다. 기저 함수는 의 품질 값이 8, 9 또는 10인 경우에 대한 것입니다. 방정식에서 BF3에 대한 계수는 115,438입니다. 이 기저 함수는 품질 값이 1에서 7 값에서 8, 9 또는 10 값으로 변경되면 모델에서 판매 가격이 $115,438 증가함을 나타냅니다. 품질 BF11 및 BF25에도 있습니다. 예측 변수가 반응 변수에 미치는 영향을 이해하려면 모든 기저 함수를 고려하십시오.
회귀 방정식
BF3 = 품질이(가) 8, 9, 10인 경우
BF6 = 최대(0, 2002 - 준공)
BF7 = 지하 1층이(가) 누락되지 않은 경우
BF10 = 최대(0, 1696 - 지하 1층) * BF7
BF11 = 품질이(가) 1, 8인 경우
BF13 = 유형이(가) 90, 150, 160, 180, 190인 경우
BF15 = 이웃이(가) 블루스템, 클리어 크릭, 크로포드, 그린 힐스, 랜드마크, 노스리지, 노스리지 하이츠, 서머셋 빌리지, 스톤 브리지, 팀버랜드, 비엔커인 경우
BF17 = 지하 총면적이(가) 누락되지 않은 경우
BF19 = 최대(0, 지하 총면적 - 1392) * BF17
BF21 = 최대(0, 1층 공간 - 2402)
BF23 = 상태이(가) 1, 2, 3, 4, 5, 6인 경우
BF25 = 품질이(가) 1, 7, 10인 경우
BF27 = 최대(0, 1층 공간 - 2207)
BF30 = 최대(0, 15138 - 로트 지역)
판매 가격 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
참고
전통적인 회귀 방정식에서 회귀 방정식의 계수는 항상 0에서 1로의 변화를 나타냅니다. 에서 MARS® 회귀 분석계수는 1에서 0으로의 변화를 나타낼 수 있습니다. 환자가 두통이 없다고 보고할 때 0이고 환자가 두통이 있다고 보고할 때 1인 이진 범주형 변수를 고려하십시오. 예측 변수에 다음과 같은 기저 함수가 있다고 가정합니다.
- BF1 = 두통이 0일 때
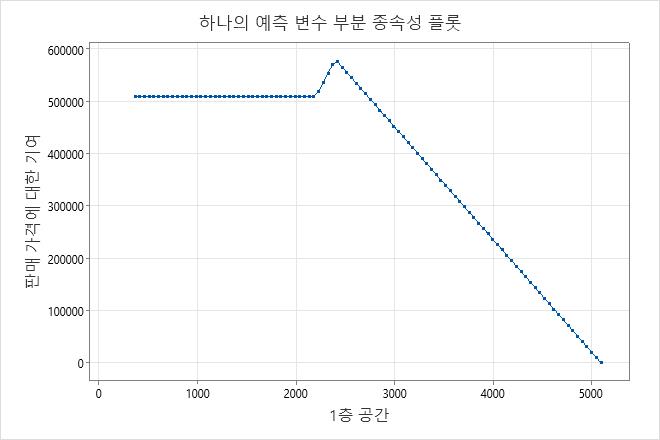
1개의 예측 변수에 대한 다중 기저 함수
MARS® 회귀 분석 단일 예측 변수에 대해 여러 기저 함수를 사용하여 예측 변수와 반응 변수 간의 더 복잡한 비선형 관계를 모형화합니다. 추가 기저 함수는 예측 변수와 반응 변수 간의 관계 기울기에 추가 변경을 생성합니다. MARS® 회귀 분석 가산 모형의 여러 기저 함수에서 예측 변수를 허용합니다.
이 결과에서 BF21은 예측 변수에 1층 공간대한 것입니다. 기본 함수 BF27은 에 대한 1층 공간것입니다. BF21 및 BF27은 모두 동일한 배열 max(0, X − c)를 갖는다. 이 배열의 기저 함수는 예측 변수의 값이 c보다 큰 경우 반응 변수에 영향을 줍니다. 이 배열을 가진 2개의 기저 함수의 경우, 예측 변수가 기저 함수 1의 최소값에 도달할 때까지 두 기저 함수 모두 반응에 영향을 주지 않습니다. 이 결과에서 이 값은 BF27에서 2,207입니다. 1층 공간 최소값에서 2,207까지의 기울기가 0입니다. 2,207 이후에는 BF27의 기울기가 적용되므로 기울기는 361.254가 됩니다. 이 기울기는 예측 변수가 BF21의 상수에 도달할 때까지 지속되며, 이 지점에서 BF27과 BF21의 계수가 모두 영향을 미칩니다 판매 가격. 두 계수의 합은 새로운 기울기 361.254 + (−576.789) = −215.535가 됩니다. 가산 모형 MARS® 회귀 분석 에서는 예측 변수의 효과를 표시하기 위해 1-예측 변수, 부분 종속성 그림을 표시합니다.
회귀 방정식
BF3 = 품질이(가) 8, 9, 10인 경우
BF6 = 최대(0, 2002 - 준공)
BF7 = 지하 1층이(가) 누락되지 않은 경우
BF10 = 최대(0, 1696 - 지하 1층) * BF7
BF11 = 품질이(가) 1, 8인 경우
BF13 = 유형이(가) 90, 150, 160, 180, 190인 경우
BF15 = 이웃이(가) 블루스템, 클리어 크릭, 크로포드, 그린 힐스, 랜드마크, 노스리지, 노스리지 하이츠, 서머셋 빌리지, 스톤 브리지, 팀버랜드, 비엔커인 경우
BF17 = 지하 총면적이(가) 누락되지 않은 경우
BF19 = 최대(0, 지하 총면적 - 1392) * BF17
BF21 = 최대(0, 1층 공간 - 2402)
BF23 = 상태이(가) 1, 2, 3, 4, 5, 6인 경우
BF25 = 품질이(가) 1, 7, 10인 경우
BF27 = 최대(0, 1층 공간 - 2207)
BF30 = 최대(0, 15138 - 로트 지역)
판매 가격 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
결측값에 대한 기저 함수
기저 함수 검색에서 결 MARS® 회귀 분석 측값이 있는 예측 변수에 대한 지표 변수를 만듭니다. 인디케이터 변수는 예측 변수의 값이 누락되었는지 여부를 보여줍니다. 분석에 모형에 결측값이 있는 예측 변수에 대한 기저 함수가 포함된 경우 모형에는 지표 변수에 대한 기저 함수도 포함됩니다. 예측 변수에 대한 다른 기저 함수는 모두 지표 변수에 대한 기저 함수와 상호 작용합니다.
예측 변수에 결측값이 있는 경우 인디케이터 변수의 기저 함수는 0을 곱하여 해당 예측 변수에 대한 다른 기저 함수를 무효화합니다. 결측값에 대한 이러한 기본 함수는 중요한 예측 변수에 결측값이 있는 모든 모형, 심지어 추가 모형과 다른 유형의 변환을 비활성화하는 모형에도 있습니다.
이 결과에서 BF7은 예측 변수에 지하 1층대한 것입니다. BF 7은 데이터에 있을 때 지하 1층 값이 1입니다. BF 7은 누락 된 경우 지하 1층 값이 0입니다. BF7은 최종 모델에서 기저 함수가 중요하지 않았기 때문에 회귀 방정식에 없지만 BF7은 BF10과 상호 작용합니다. BF10은 중요하며 회귀 방정식에 존재합니다. BF7의 효과는 누락되었을 때 지하 1층 BF10에 0을 곱하여 누락되었을 때 지하 1층 효과를 제거하는 것입니다.
회귀 방정식
BF3 = 품질이(가) 8, 9, 10인 경우
BF6 = 최대(0, 2002 - 준공)
BF7 = 지하 1층이(가) 누락되지 않은 경우
BF10 = 최대(0, 1696 - 지하 1층) * BF7
BF11 = 품질이(가) 1, 8인 경우
BF13 = 유형이(가) 90, 150, 160, 180, 190인 경우
BF15 = 이웃이(가) 블루스템, 클리어 크릭, 크로포드, 그린 힐스, 랜드마크, 노스리지, 노스리지 하이츠, 서머셋 빌리지, 스톤 브리지, 팀버랜드, 비엔커인 경우
BF17 = 지하 총면적이(가) 누락되지 않은 경우
BF19 = 최대(0, 지하 총면적 - 1392) * BF17
BF21 = 최대(0, 1층 공간 - 2402)
BF23 = 상태이(가) 1, 2, 3, 4, 5, 6인 경우
BF25 = 품질이(가) 1, 7, 10인 경우
BF27 = 최대(0, 1층 공간 - 2207)
BF30 = 최대(0, 15138 - 로트 지역)
판매 가격 = 325577 - 57.6167 * BF2 + 115438 * BF3 - 605.079 * BF6 - 25.3989 * BF10 - 66735.2 *
BF11 - 23688.9 * BF13 + 22374.5 * BF15 + 50.3801 * BF19 - 576.789 * BF21 - 18099.2 * BF23 +
22414.2 * BF25 + 361.254 * BF27 - 1.82 * BF30
상호 작용의 기본 함수
교호작용을 MARS® 회귀 분석 모형화하려면 여러 예측 변수에 대한 기저 함수를 곱합니다. MARS® 회귀 분석 기본 가산 모형의 교호작용을 고려하지 않습니다. 부분 종속성 그림은 교호작용을 고려하는 분석에 사용할 수 없습니다.
교호작용은 예측 변수의 효과가 다른 예측 변수의 값에 따라 달라진다는 것을 의미합니다. 예를 들어, 오븐에서 곡물이 건조되는 속도는 오븐에서의 시간에 따라 다르지만 시간의 영향은 오븐의 온도에 따라 다릅니다. 시간 변수와 온도 변수가 상호 작용합니다.
교호작용이 있는 모형에 대한 결과에서 BF9는 예측 변수에 품질대한 것입니다. BF12는 예측 변수에 1층 공간대한 것입니다. BF12의 계산에는 BF9에 의한 곱셈이 포함되므로 두 예측 변수가 상호 작용합니다. 다른 예측 변수의 효과 품질 에 대한 결정이나 1층 공간 다른 예측 변수의 값에 대한 지식이 필요합니다. -63.1685의 BF12에 대한 계수는 BF9의 값이 1인 경우에만 적용됩니다. BF9의 값은 8, 9 또는 10일 때 품질 1입니다. BF12 1층 공간 의 배열로 인해 평방 피트가 63.1685보다 작고 값이 품질 8, 9 또는 10일 때 기울기가 10입니다.
회귀 방정식
BF4 = 최대(0, 2002 - 준공)
BF5 = 지하 1층이(가) 누락되지 않은 경우
BF7 = 최대(0, 지하 1층 - 1758) * BF5
BF8 = 최대(0, 1758 - 지하 1층) * BF5
BF9 = 품질이(가) 8, 9, 10인 경우
BF12 = 최대(0, 2470 - 1층 공간) * BF9
BF14 = 품질이(가) 7, 9, 10인 경우
BF15 = 유형이(가) 75, 90, 150, 160, 180, 190인 경우
BF19 = 이웃이(가) 블루스템, 클리어 크릭, 크로포드, 그린, 그린 힐스, 노스리지, 노스리지 하이츠, 서머셋 빌리지, 스톤 브리지, 팀버랜드, 비엔커인 경우 *
BF5
BF21 = 상태이(가) 1, 2, 3, 4, 5, 6인 경우 * BF4
BF25 = 최대(0, 1층 공간 - 372) * BF7
BF26 = 지하 총면적이(가) 누락되지 않은 경우 * BF14
BF28 = 최대(0, 지하 총면적 - 689) * BF26
판매 가격 = 320349 - 66.4387 * BF2 - 28.2065 * BF8 + 123645 * BF9 - 63.1685 * BF12 - 23751.7 *
BF15 + 22818.2 * BF19 - 523.924 * BF21 - 0.036887 * BF25 + 53.9878 * BF28
