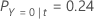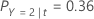분류 트리는 원래 학습 데이터 세트의 이항 재귀 분할에서 발생합니다. 트리의 모든 부모 노드(학습 데이터의 부분 집합)는 노드에서 수집된 실제 데이터 값에 따라 다양한 방법으로 상호 배타적인 두 개의 자식 노드로 분할될 수 있습니다.
분할 절차는 예측 변수를 계량형 또는 범주형으로 처리합니다. 계량형 변수 X와 값 c의 경우 x 값이 c보다 작거나 같은 모든 레코드를 왼쪽 노드에 보내고 나머지 모든 레코드를 오른쪽 노드로 전송하여 분할이 정의됩니다. CART는 항상 두 개의 인접 값 평균을 사용하여 c를 계산합니다. N개의 고유값이 있는 계량형 변수는 부모 노드의 N-1 잠재적 분할을 생성합니다(허용된 최소 노드 크기에 대한 제한이 지정되면 실제 숫자는 더 작아집니다).
예를 들어 계량형 예측 변수의 데이터에는 55, 66 및 75 값이 있습니다. 이 변수에 대한 가능한 분할 중 하나는 모든 값을 (55+66)/2 = 60.5 이하의 모든 값을 한 자식 노드에 보내고 60.5보다 큰 모든 값을 다른 자식 노드로 보내는 것입니다. 예측 변수 값이 55인 사례는 한 노드로 이동하고 값이 66과 75인 사례는 다른 노드로 이동합니다. 이 예측 변수에 대한 다른 가능한 분할은 70.5 이하의 모든 값을 한 자식 노드에 보내고 70.5보다 큰 값을 다른 노드로 보내는 것입니다. 값이 55와 66인 사례는 한 노드로 이동하고 값이 75인 사례는 다른 노드로 이동합니다.
고유값 {c0, c2, …, ck}를 가진 범주형 변수 X의 경우, 분할은 왼쪽 자식 노드로 전송되는 수준의 부분 집합으로 정의됩니다. K 수준이 있는 범주형 변수는 최대 2개 생성됩니다.K-1-1 분할.
| 왼쪽 자식 노드 | 오른쪽 자식 노드 |
|---|---|
| 빨강, 파랑 | 노랑 |
| 빨강, 노랑 | 파랑 |
| 파랑, 노랑 | 빨강 |
분류 트리에서 목표값은 K 고유 클래스를 가진 다항입니다. 트리의 주요 목표는 최대한 순수한 방법을 사용하여 개별 노드로 다른 목표 클래스를 구분하는 방법을 찾는 것입니다. 결과 터미널 노드 수는 K일 필요가 없습니다. 여러 터미널 노드를 사용하여 특정 목표 클래스를 나타낼 수 있습니다. 사용자는 목표 클래스에 대한 사전 확률을 지정할 수 있으며, 트리 성장 과정에서 CART에 의해 설명됩니다.
다음 섹션에서 Minitab은 이항 반응 변수에 대해 다음 정의를 사용합니다.
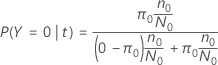
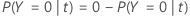
다음 섹션에서 Minitab은 다항 반응 변수에 대해 다음 정의를 사용합니다.
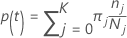
클래스 확률 j 주어진 노드 t:
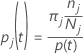
이러한 정의는 노드 내 확률을 제공합니다. Minitab은 모든 노드 및 잠재적 분할에 대한 이러한 확률을 계산합니다. Minitab은 다음 기준 중 하나를 사용하여 이러한 확률에서 분할될 수 있는 잠재적인 분할에 대한 전반적인 개선을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| K | 반응 변수의 클래스 수 |
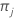 | 클래스에 대한 사전 확률 j |
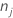 | 클래스에 대한 관측치 수 j 노드에서 |
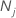 | 클래스에 대한 관측치 수 j 데이터에서 |
지니 기준
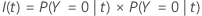
다음보다 일반적인 수식은 다항 반응 변수에 적용됩니다.
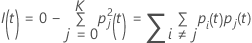
노드에 대한 모든 관측치가 한 클래스에 있는 경우  .
.
엔트로피 기준
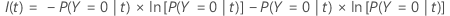
다음보다 일반적인 수식은 다항 반응 변수에 적용됩니다.
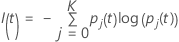
노드에 대한 모든 관측치가 한 클래스에 있는 경우  .
.
투잉 기준
| 슈퍼 클래스 1 | 슈퍼 클래스 2 |
|---|---|
| 1, 2, 3 | 4(4) |
| 1, 2, 3 | 3(3) |
| 1, 3, 4 | 2 |
| 2, 3, 4 | 0 |
| 1, 2 | 3, 4 |
| 1, 3 | 2, 4 |
| 1, 4 | 2, 3 |

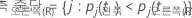
왼쪽 슈퍼 클래스에는 왼쪽으로 이동하는 경향이 있는 모든 목표 클래스가 있습니다. 올바른 슈퍼 클래스에는 오른쪽으로 이동하는 경향이 있는 모든 목표 클래스가 있습니다.
| 클래스 | 왼쪽 자식 노드 확률 | 오른쪽 자식 노드 확률 |
|---|---|---|
| 0 | 0.67 | 0.33 |
| 2 | 0.82 | 0.18 |
| 3(3) | 0.23 | 0.77 |
| 4(4) | 0.89 | 0.11 |
그런 다음 후보 분할에 대한 슈퍼 클래스를 만드는 가장 좋은 방법은 {1, 2, 4}를 하나의 슈퍼 클래스로 할당하고 {3}를 다른 슈퍼 클래스로 할당하는 것입니다.
계산의 나머지는 이항 목표로 슈퍼 클래스와 지니 기준에 대해 동일합니다.
기준에 대한 개선 계산
Minitab이 노드 불순도를 계산한 후 Minitab은 노드를 예측 변수로 분할하기 위한 조건부 확률을 계산합니다.
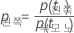
및
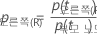
그런 다음 분할에 대한 개선은 다음 수식에서 얻습니다.
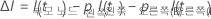
개선 값이 가장 높은 분할은 트리의 일부가 됩니다. 두 예측 변수의 개선이 동일하면 알고리즘을 계속하려면 선택이 필요합니다. 선택 영역은 워크시트의 예측 변수 위치, 예측 변수 유형 및 범주형 예측변수의 클래스 수를 포함하는 결정적 타이 브레이킹 스키마를 사용합니다.
클래스 확률
노드 분할은 지정된 노드 내에서 클래스 확률을 최대화합니다.
터미널 노드
- 노드의 사례 수가 해석의 최소 크기에 도달합니다. Minitab Statistical Software의 기본 최소값은 3입니다.
- 노드의 모든 사례에는 동일한 반응 클래스가 있습니다.
- 노드의 모든 사례에는 동일한 예측 변수 값이 있습니다.
터미널 노드에 대한 예측 클래스
터미널 노드에 대한 예측 클래스는 노드의 오분류 비용을 최소화하는 클래스입니다. 오분류 비용의 표현은 반응 변수의 클래스 수에 따라 달라집니다. 터미널 노드에 대한 예측 클래스는 검증 방법을 사용할 때 학습 데이터에서 비롯되므로 다음의 모든 수식은 학습 데이터 세트의 확률을 사용합니다.
이항 반응 변수
다음 방정식은 노드의 사례가 사건 클래스라는 예측에 대한 오분류 비용을 제공합니다.
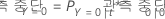
다음 방정식은 노드의 사례가 비사건 클래스라는 예측에 대한 오분류 비용을 제공합니다.
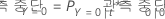
| 용어 | 설명 |
|---|---|
| PY=0|t | 노드의 사례인 경우 조건부 확률 t 비사건 클래스에 속합니다. |
| 관측 중단1|0 | 비사건 클래스 사례를 사건 클래스 사례로 예측하는 오분류 비용 |
| PY=1|t | 노드의 사례인 경우 조건부 확률 t 사건 클래스에 속합니다. |
| 관측 중단0|1 | 사건 클래스 사례를 비사건 클래스 사례로 예측하는 오분류 비용 |
터미널 노드에 대한 예측 클래스는 최소 오분류 비용이 있는 클래스입니다.
다항 반응 변수

예를 들어 세 가지 클래스와 다음과 같은 오분류 비용이 있는 반응 변수를 고려합니다.
| 예측 클래스 | |||
| 실제 클래스 | 0 | 2 | 3(3) |
| 0 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3(3) | 0.4 | 0.9 | 0.0 |
그런 다음 반응 변수의 클래스에 노드에 대한 다음과 같은 확률이 있음을 고려하십시오. t:
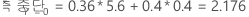

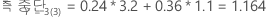
가장 낮은 오분류 비용은 예측 Y = 3, 1.164에 대한 것입니다. 이 클래스는 터미널 노드에 대한 예측 클래스입니다.