중요한 예측 변수
모든 분류 트리는 분할의 컬렉션입니다. 각 분할은 트리를 개선합니다. 각 분할에는 트리를 개선하는 대체 분할도 포함됩니다. 트리가 변수를 사용하여 노드를 분할하거나 다른 변수에 결측값이 있을 때 노드를 분할하는 대체로 변수의 중요도가 부여됩니다.
다음 수식은 단일 노드에서 개선된 기능을 제공합니다.
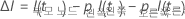
I(t), pLeft 및 pRight 값은 노드 분할 기준에 따라 달라집니다. 자세히 알려면 노드 분할 방법 CART® 분류(으)로 이동하십시오.

평균 로그 우도
학습 데이터 또는 검증 없음
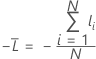
설명
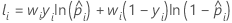
학습 데이터 표기법 또는 검증 없음
| 용어 | 설명 |
|---|---|
| N | 전체 데이터 또는 학습 데이터의 표본 크기 |
| wi | 전체 또는 학습 데이터 세트의 i번째 관측치의 가중치 |
| yi | 사건에 대해 1이고 전체 또는 학습 데이터 세트에서 0인 지시 변수 |
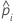 | 전체 또는 학습 데이터 세트의 i번째 행에 대한 사건의 예측 확률 |
K-접기 교차 검증
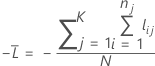
설명

k-접기 교차 검증 표기법
| 용어 | 설명 |
|---|---|
| N | 전체 또는 학습 데이터의 표본 크기 |
| nj | 접기 j의 표본 크기 |
| wij | 접기 j의 i번째 관측치에 대한 가중치 |
| yij | 사건에 대해 1이고 접기 j의 데이터에 대해 0인 지시 변수 |
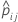 | 접기 j의 i번째 관측치를 포함하지 않는 모형 추정에서 사건의 예측 확률 |
검정 데이터 세트
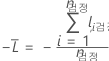
설명
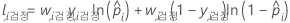
검정 데이터 세트 표기법
| 용어 | 설명 |
|---|---|
| nTest | 검정 세트의 표본 크기 |
| wi, Test | 검정 데이터 세트의 i번째 관측치에 대한 가중치 |
| yi, Test | 사건에 대해 1이고 검정 세트의 데이터에 대해 0인 지시 변수 |
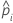 | 검정 세트에서 i번째 행에 대한 사건 예측 확률 |
ROC 곡선 아래 면적
수식


곡선 아래의 면적에 대해 Minitab은 통합을 사용합니다.

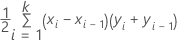
여기서 k는 터미널 노드의 수이고 (x0, y0)은 점(0, 0)입니다.
| x(가양성률) | y(진양성률) |
|---|---|
| 0.0923 | 0.3051 |
| 0.4154 | 0.7288 |
| 0.7538 | 0.9322 |
| 1 | 1 |
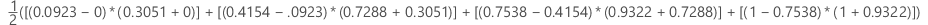

표기법
| 용어 | 설명 |
|---|---|
| TRP | 진양성률 |
| FPR | 가양성률 |
| TP | 진양성, 올바르게 평가된 사건 |
| P | 실제 긍정적인 사건의 수 |
| FP | 진음성, 올바르게 평가된 비사건 |
| N | 실제 부정적인 사건 수 |
| FNR | 가음성률 |
| TNR | 진음성률 |
ROC 곡선 아래 면적에 대한 95% CI
다음 간격은 신뢰 구간에 대한 상한 및 하한을 제공합니다.
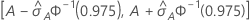
ROC 곡선 아래 면적의 표준 오차 계산(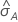 )은 Salford Predictive Modeler®에서 제공됩니다. ROC 곡선 아래의 면적 분산 추정에 대한 일반적인 정보는 다음 참조 자료를 참고하십시오.
)은 Salford Predictive Modeler®에서 제공됩니다. ROC 곡선 아래의 면적 분산 추정에 대한 일반적인 정보는 다음 참조 자료를 참고하십시오.
Engelmann, B. (2011). Measures of a ratings discriminative power: Applications and limitations. In B. Engelmann & R. Rauhmeier (Eds.), The Basel II Risk Parameters: Estimation, Validation, Stress Testing - With Applications to Loan Risk Management (2nd ed.) Heidelberg; New York: Springer. doi:10.1007/978-3-642-16114-8
Cortes, C. and Mohri, M. (2005). Confidence intervals for the area under the ROC curve. Advances in neural information processing systems, 305-312.
Feng, D., Cortese, G., & Baumgartner, R. (2017). 작은 표본 크기의 연속 진단 검정을 위해 ROC 곡선 아래의 면적에 대한 신뢰도/신뢰할 수 있는 구간 방법의 비교입니다. Statistical Methods in Medical Research, 26(6), 2603-2621. doi:10.1177/0962280215602040
표기법
| 용어 | 설명 |
|---|---|
| A | ROC 곡선 아래 면적 |
 | 표준 정규 분포의 0.975 백분위수 |
향상도
수식
사건 등급에 할당될 확률이 가장 높은 데이터에 있는 관측치의 10%에 대해 다음 수식을 사용합니다.
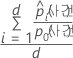
검정 데이터 세트가 있는 검정 향상도의 경우 검정 데이터 세트의 관측치를 사용합니다. k-접기 교차 검증을 사용한 검정 향상도의 경우 사용할 데이터를 선택하고 모형 추정에 없는 데이터에 대한 예측 확률에서 향상도를 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| d | 데이터의 10%에 있는 사례 수 |
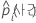 | 사건의 예측 확률 |
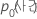 | 학습 데이터 또는 분석에서 검증을 사용하지 않는 경우 전체 데이터 세트에서 사건의 확률 |
오분류 비용
모형 요약 표의 오분류 비용은 모든 관측치를 가장 빈번한 등급으로로 분류하는 사소한 분류기와 관련된 모형의 상대적 분류 비용입니다.
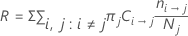
상대적 오분류 비용의 형식은 다음과 같습니다.
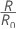
여기서 R0은 사소한 분류기의 비용입니다.
사전 확률이 같거나 데이터에서 제공된 경우 R 수식이 단순화됩니다.
사전 확률이 같음

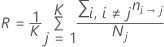
데이터의 사전 확률

이 정의를 사용하면 R의 형식은 다음과 같습니다.
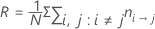
표기법
| 용어 | 설명 |
|---|---|
| πj | 반응 변수의 j번째 등급의 사전 확률 |
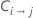 | 등급 i를 등급 j로 오분류하는 비용 |
 | 등급 j로 오분류된 등급 i의 레코드 수 |
| Nj | 반응 변수의 j번째 등급에 있는 사례 수 |
| K | 반응 변수의 등급 수 |
| N | 데이터의 사례 수 |
