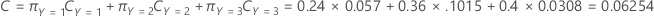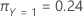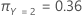분할 방법이 클래스 확률인 경우 오분류 표가 없습니다.
카운트
가중치가 없는 경우 개수와 표본 크기는 동일합니다.
가중 카운트
가중치가 있는 사례에서 가중 카운트는 범주에 대한 가중치의 합계입니다. 가장 가까운 실수로 반올림한 가중 카운트 반올림되지 않은 가중치를 사용하여 백분율과 비율을 계산합니다. 다음의 간단한 예를 고려해 보십시오.
| 응답 수준 | 예측 수준 | 가중치 |
|---|---|---|
| 예 | 예 | 0.1 |
| 예 | 예 | 0.2 |
| 예 | 아니요 | 0.3 |
| 예 | 아니요 | 0.4 |
| 아니요 | 아니요 | 0.5 |
| 아니요 | 아니요 | 0.6 |
| 아니요 | 예 | 0.7 |
| 아니요 | 예 | 0.8 |
이 표는 다음과 같은 통계를 제공합니다.
| 실제 클래스 | 가중 카운트 | 오분류됨 | 예측 클래스 = 아니요 | 백분율 수정 |
|---|---|---|---|---|
| 예 | 0.1 + 0.2 + 0.3 + 0.4 = 1 | 0.1 + 0.2 = 0.3 ≈ 0 | 0.3 + 0.4 = 0.7 ≈ 1 | (0.3 / 1.0) ×100 = 30% |
| 아니요 | 0.5 + 0.6 + 0.7 + 0.8 = 2.6 ≈ 3 | 0.7 + 0.8 = 1.5 ≈ 2 | 0.5 + 0.6 = 1.1 ≈ 1 | 1.1 / 2.6) × 100 = 42.31% |
| 모두 | 1 + 2.6 = 3.6 ≈ 4 | 0.3 + 1.5 = 1.8 ≈ 2 | 0.7 + 1.1 = 1.8 ≈ 2 | (0.3 + 1.1) / 3.6 × 100 = 38.89% |
오차율(%)
가중치가 있는 사례에서 개수 대신 가중 카운트를 사용합니다.
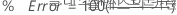
비용
비용 계산은 반응 변수가 이항인지 다항인지에 따라 달라집니다.
비용 = (% 오류 × 클래스의 오분류 비용 입력) / 100
이항 반응 변수
다음 방정식은 사건 클래스에 대한 비용을 제공합니다.

다음 방정식은 비사건 클래스에 대한 비용을 제공합니다.

다음 방정식은 모든 클래스에 대한 전체 비용을 제공합니다.

다항 반응 변수
다항 사례의 경우 방정식은 가능한 모든 오분류 유형을 고려하여 이항 반응 변수에 대한 수식을 확장합니다. 예를 들어 k 클래스를 사용하는 다중 공응답의 경우 Y = 1의 오분류 비용은 다음 방정식을 사용합니다.
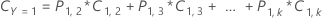
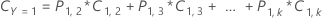
다음 방정식은 다항 사례에 대한 전체 비용을 제공합니다.

예를 들어 3개의 클래스와 다음과 같은 오분류 비용이 있는 반응 변수를 고려합니다.
| 예측 클래스 | |||
| 실제 클래스 | 1 | 2 | 3 |
| 1 | 0.0 | 4.1 | 3.2 |
| 2 | 5.6 | 0.0 | 1.1 |
| 3 | 0.4 | 0.9 | 0.0 |
그런 다음 다음 표에서 오차 백분율을 제공합니다.
| 예측 클래스 | |||
| 실제 클래스 | 1 | 2 | 3 |
| 1 | 사용할 수 없음 | 1% | 0.5% |
| 2 | 1.4% | 사용할 수 없음 | 2.1% |
| 3 | 5% | 1.2% | 사용할 수 없음 |
마지막으로 반응 변수의 클래스에 다음과 같은 사전 확률이 있음을 고려하십시오.
다음 방정식은 반응 변수의 각 클래스에 대한 오분류와 관련된 비용을 제공합니다.






다음 방정식은 전체 비용을 제공합니다.