고유값
고유값(특성값 또는 잠재근이라고도 함)은 주성분의 분산입니다.
해석
고유값 크기를 사용하여 주성분 수를 결정할 수 있습니다. 고유값이 가장 큰 주성분을 유지합니다. 예를 들어, Kaiser 기준을 사용하는 경우 고유값이 1보다 큰 주성분만 사용합니다.
고유값 크기를 시각적으로 비교하려면 Scree 그림을 사용하십시오. Scree 그림은 고유값 크기를 기반으로 성분 수를 결정하는 데 도움이 됩니다.
상관 행렬에 대한 고유 분석
| 고유값 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 비율 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 누적 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
고유 벡터
| 변수 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 수입 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 교육 수준 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 나이 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 거주 기간 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 근무 기간 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 저축 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 부채 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 신용카드 수 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
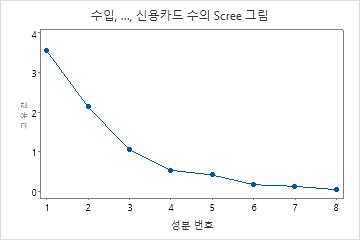
이 결과에서는 처음 세 주성분의 값이 1보다 큽니다 이 세 성분이 데이터 변동의 84.1%를 설명합니다. Scree 그림은 고유값들이 세 번째 주성분 다음에 직선을 형성하기 시작한다는 것을 보여줍니다. 84.1%가 데이터에서 설명되는 적절한 변동량인 경우 처음 세 주성분을 사용해야 합니다.
비율
비율은 각 주성분에 의해 설명되는 데이터 변동성의 비율입니다.
해석
비율을 사용하여 데이터 변동성의 대부분을 설명하는 주성분을 확인할 수 있습니다. 비율이 높을수록 주성분이 변동성을 더 많이 설명합니다. 비율 크기는 주성분이 유지하기에 충분히 중요한지 여부를 결정하는 데 도움이 됩니다.
예를 들어, 비율이 0.621인 주성분은 데이터 변동성의 62.1%를 설명합니다. 따라서 이 성분은 포함할 만큼 중요합니다. 또 다른 성분은 비율이 0.005로, 데이터 변동성의 0.5%만 설명합니다. 이 성분은 포함할 만큼 중요하지 않을 수 있습니다.
누적
누적은 연속적인 주성분들이 설명하는 표본 변동성의 누적 비율입니다.
해석
누적 비율을 사용하면 연속적인 주성분들이 설명하는 전체 분산 양을 평가할 수 있습니다. 누적 비율은 사용할 주성분의 수를 결정하는 데 도움이 됩니다. 허용 가능한 분산 수준을 설명하는 주성분을 유지합니다. 허용 수준은 연구에 따라 다릅니다.
예를 들어, 설명을 위해서만 사용할 경우 주성분들이 분산의 80%만 설명하면 됩니다. 그러나 데이터에 대해 다른 분석을 수행하는 경우에는 주성분들이 분산의 90% 이상을 설명할 수도 있습니다.
주성분(PC)
참고
상관 행렬을 사용하는 경우 올바른 성분 점수를 얻으려면 변수를 표준화해야 합니다.
해석
각 주성분을 해석하려면 원래 변수 계수의 크기와 계수를 조사합니다. 계수의 절대값이 클수록 성분을 구성할 때 해당 변수의 중요성도 커집니다. 중요한 것으로 간주되기 위한 계수의 절대값 크기는 주관적입니다. 상관 계수 값이 중요한 수준을 확인하려면 전문 지식을 활용합니다.
상관 행렬에 대한 고유 분석
| 고유값 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 비율 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 누적 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
고유 벡터
| 변수 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 수입 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 교육 수준 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 나이 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 거주 기간 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 근무 기간 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 저축 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 부채 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 신용카드 수 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
이 결과에서 첫 번째 주성분은 나이, 거주, 직장 및 저축과 큰 양의 연관성이 있습니다. 이 성분을 신청자의 장기적인 재정 안정성에 대한 주요 측정값으로 해석할 수 있습니다. 두 번째 성분은 부채 및 신용카드와 큰 음의 연관성이 있으므로 주로 신청자의 신용 정보를 측정합니다. 세 번째 성분은 수입, 교육 수준 및 신용카드와 큰 음의 연관성이 있으므로 주로 신청자의 교육 및 직업 조건을 측정합니다.
점수
점수는 각 주성분에 대한 계수에 의해 결정되는 데이터의 선형 결합입니다. 각 관측치에 대한 점수를 얻으려면 주성분에 대한 선형 방정식에서 값을 대체하십시오. 상관 행렬을 사용하는 경우 선형 방정식을 사용할 때 정확한 성분 점수를 얻으려면 변수를 표준화해야 합니다.
참고
각 관측치에 대해 계산된 점수를 얻으려면 분석을 수행할 때 저장을 클릭하고 점수를 저장할 워크시트의 열을 입력하십시오. 첫 번째와 두 번째 성분에 대한 점수를 그래프에 시각적으로 표시하려면 분석을 수행할 때 그래프을 클릭하고 점수 그림을 선택하십시오.
상관 행렬에 대한 고유 분석
| 고유값 | 3.5476 | 2.1320 | 1.0447 | 0.5315 | 0.4112 | 0.1665 | 0.1254 | 0.0411 |
|---|---|---|---|---|---|---|---|---|
| 비율 | 0.443 | 0.266 | 0.131 | 0.066 | 0.051 | 0.021 | 0.016 | 0.005 |
| 누적 | 0.443 | 0.710 | 0.841 | 0.907 | 0.958 | 0.979 | 0.995 | 1.000 |
고유 벡터
| 변수 | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 |
|---|---|---|---|---|---|---|---|---|
| 수입 | 0.314 | 0.145 | -0.676 | -0.347 | -0.241 | 0.494 | 0.018 | -0.030 |
| 교육 수준 | 0.237 | 0.444 | -0.401 | 0.240 | 0.622 | -0.357 | 0.103 | 0.057 |
| 나이 | 0.484 | -0.135 | -0.004 | -0.212 | -0.175 | -0.487 | -0.657 | -0.052 |
| 거주 기간 | 0.466 | -0.277 | 0.091 | 0.116 | -0.035 | -0.085 | 0.487 | -0.662 |
| 근무 기간 | 0.459 | -0.304 | 0.122 | -0.017 | -0.014 | -0.023 | 0.368 | 0.739 |
| 저축 | 0.404 | 0.219 | 0.366 | 0.436 | 0.143 | 0.568 | -0.348 | -0.017 |
| 부채 | -0.067 | -0.585 | -0.078 | -0.281 | 0.681 | 0.245 | -0.196 | -0.075 |
| 신용카드 수 | -0.123 | -0.452 | -0.468 | 0.703 | -0.195 | -0.022 | -0.158 | 0.058 |
이 결과에서 첫 번째 주성분에 대한 점수는 PC1 아래 나열된 계수를 사용하여 표준화된 데이터에서 계산할 수 있습니다.
PC1 = 0.314 수입 + 0.237 교육 + 0.484 나이 + 0.466 거주지 + 0.459 직장 + 0.404 저축 - 0.067 부채 - 0.123 신용카드
거리
Mahalanobis 거리는 데이터 점과 다변량 공간의 중심(전체 평균) 사이의 거리입니다.
참고
각 관측치에 대한 거리를 계산하려면 분석을 수행할 때 저장을 클릭하고 거리를 저장할 워크시트의 열을 입력하십시오. 거리를 그래프에 표시하려면 분석을 수행할 때 그래프을 클릭한 다음 특이치 그림을 선택하십시오.
해석
Mahalanobis 거리를 사용하면 특이치를 식별할 수 있습니다. Mahalanobis 거리를 조사하는 것은 거리가 변수 간에 서로 다른 척도 및 상관 관계를 고려하기 때문에 특이치를 탐지하는 데 있어 한 번에 하나의 변수를 조사하는 것보다 더 강력한 다변량 방법입니다.
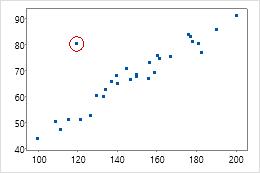
예를 들어, 개별적으로 고려할 경우 원으로 표시되는 데이터 점의 x-값 및 y-값이 비정상적이지 않습니다. 그러나 데이터 점은 두 변수의 상관 관계 구조에 적합하지 않습니다. 따라서 이 점에 대한 Mahalanobis 거리가 비정상적으로 큽니다.
거리 값이 관측치를 특이치로 간주할 만큼 충분히 큰지 여부를 평가하려면 특이치 그림을 사용하십시오.
Scree 그림
Scree 그림은 주성분 번호와 해당 고유값을 표시합니다. Scree 그림은 고유값을 가장 큰 값에서 가장 작은 값의 순서로 정렬합니다. 상관 행렬의 고유값은 주성분의 분산과 같습니다.
Scree 그림을 표시하려면 분석을 수행할 때 그래프을 클릭하고 Scree 그림을 선택합니다.
해석

이 Scree 그림은 고유값들이 세 번째 주성분 다음에 직선을 형성하기 시작한다는 것을 보여줍니다. 따라서 나머지 주성분은 변동성의 아주 작은 부분(0에 가까움)을 설명하므로 중요하지 않을 수 있습니다.
점수 그림
점수 그림은 두 번째 주성분 점수 대 첫 번째 주성분 점수를 그래프로 나타낸 것입니다.
점수 그림을 표시하려면 분석을 수행할 때 그래프을 클릭하고 점수 그림을 선택합니다.
해석
처음 두 성분이 데이터에서 분산의 대부분을 설명하는 경우에는 점수 그림을 사용해도 데이터 구조를 평가할 수 있고 군집, 특이치 및 추세를 탐지할 수 있습니다. 그림의 데이터 그룹은 데이터에 둘 이상의 개별 분포가 존재한다는 것을 나타낼 수도 있습니다. 데이터가 정규 분포를 따르고 특이치가 없는 경우 점들은 0 주위에 랜덤하게 분포합니다.
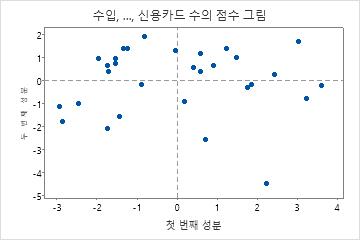
이 점수 그림에서 하단 구석에 있는 점이 특이치일 수 있습니다. 이 점을 조사해야 합니다.
팁
각 관측치에 대해 계산된 점수를 보려면 포인터를 그래프의 데이터 점 위에 놓으십시오. 다른 성분에 대한 점수 그림을 생성하려면 점수를 저장하고 을 사용하십시오.
적재 그림
적재 그림은 첫 번째 성분에 대한 각 변수의 계수 대 두 번째 성분에 대한 계수를 그래프로 표시합니다. 계수는 각 주성분에 대한 고유벡터를 구성하는 값입니다. 계수는 성분에서 각 변수의 상대적인 가중치를 나타냅니다.
적재 그림을 표시하려면 분석을 수행할 때 그래프을 클릭하고 적재 그림을 선택합니다.
해석
적재 그림을 사용하면 각 성분에 가장 큰 영향을 미치는 변수를 식별할 수 있습니다. 계수의 범위는 -1에서 1 사이입니다. 계수가 -1 또는 1에 가까우면 변수가 성분에 큰 영향을 미친다는 것을 나타냅니다. 계수가 0에 가까우면 변수가 성분에 미치는 영향이 약하다는 것을 나타냅니다. 계수를 평가하면 변수의 관점에서 각 성분을 특성화하는 데도 도움이 될 수 있습니다.
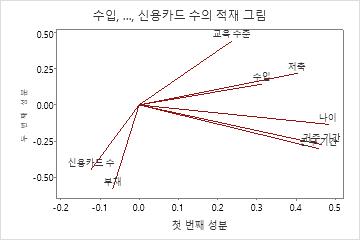
이 계수 그림에서 나이, 거주, 직장 및 저축은 성분 1에 큰 음의 적재가 되므로 이 성분은 주로 신청자의 재정 안정성을 측정합니다. 부채 및 신용 카드는 성분 2에서 음의 계수가 크므로 이 성분은 주로 신청자의 신용 기록을 측정합니다.
행렬도
행렬도는 점수 그림과 적재 그림을 겹쳐서 표시합니다.
행렬도를 표시하려면 분석을 수행할 때 그래프을 클릭하고 행렬도를 선택하십시오.
해석
행렬도를 사용하여 데이터 구조와 처음 두 성분의 적재를 한 그래프에 나타낼 수 있습니다. Minitab에서는 두 번째 주성분 점수 대 첫 번째 주성분 점수 및 두 성분에 대한 적재를 그림으로 표시합니다.
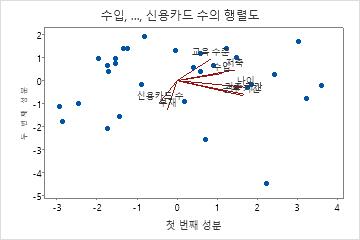
- 나이, 거주, 직장 및 저축은 성분 1에 큰 음의 적재가 되므로 이 성분은 신청자의 장기적인 재정 안정성에 초점을 맞춥니다.
- 부채 및 신용카드는 성분 2에 큰 음의 적재가 되므로 이 성분은 신청자의 신용 정보에 초점을 맞춥니다.
- 오른쪽 하단 구석에 있는 점이 특이치일 수 있습니다. 이 점을 조사해야 합니다.
특이치 그림
특이치 그림은 특이치를 나타내기 위해 각 관측치에 대한 Mahalanobis 거리 및 기준선을 표시합니다. Mahalanobis 거리는 각 데이터 점과 다변량 공간의 중심(전체 평균) 사이의 거리입니다. Mahalanobis 거리를 조사하는 것은 변수 간에 서로 다른 척도와 상관 관계를 고려하기 때문에 특이치를 탐지하는 데 있어 한 번에 하나의 변수를 조사하는 것보다 더 강력한 방법입니다.
특이치 그림을 표시하려면 분석을 수행할 때 그래프을 클릭하고 특이치 그림을 선택해야 합니다.
해석
특이치 그림을 사용하면 특이치를 식별할 수 있습니다. 기준선 위에 있는 점은 특이치입니다.
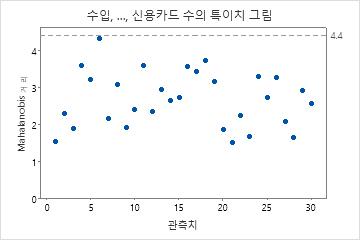
이 결과에는 특이치가 없습니다. 모든 점이 기준선 아래에 있습니다.
팁
관측치를 식별하려면 특이치 그림의 점 위에 포인터를 놓으십시오. 그림의 여러 특이치를 브러시하고 워크시트의 관측치를 표시하려면 을 사용하십시오.
