주성분
주성분 추출 방법에서 j번째 적재는 j번째 주성분의 척도화된 계수입니다. 인자는 처음 m개의 성분과 관련이 있습니다. 회전되지 않은 솔루션에서 주성분 분석에서 성분을 해석하는 것처럼 인자를 해석할 수 있습니다. 그러나 회전 후에는 인자를 더 이상 주성분과 유사하게 해석할 수 없습니다.
표본 상관 행렬 R(또는 공분산 행렬 S)의 주성분 인자 분석은 고유값-고유 벡터 쌍(λi, ei)의 관점에서 지정됩니다(i = 1, ...,p 및 λ1 ≤ λ2 ≤ ... ≤ λp). m < p를 공통 인자의 수로 정의합니다. 추정된 인자 적재의 행렬은 i번째 열이 다음과 같은 p × m 행렬, L입니다.  , i = 1, ..., m.
, i = 1, ..., m.
최대우도법
최대우도 방법은 인자 적재를 추정하며, 데이터가 다변량 정규 분포를 따른다고 가정합니다. 최대우도라는 이름이 의미하듯이 이 방법은 다변량 정규 모형과 연관된 우도 함수를 최대화하여 인자 적재와 고유 분산의 추정치를 찾습니다. 또는 잔차의 분산이 포함된 식을 최소화하여 추정치를 찾습니다. 최소값을 찾거나 지정된 최대 반복 횟수(기본값 25)에 도달할 때까지 알고리즘이 반복됩니다.
Minitab에서는 Joreskog,1,2을 기반으로 한 알고리즘을 약간 수정하여 수렴 개선에 사용합니다. 여기에 알고리즘의 간략한 요약을 제공합니다.
p개의 변수가 있고 m개의 인자를 사용하여 모형을 적합한다고 가정합니다. R를 변수의 p × p 상관 행렬, L을 인자 적재의 p × m 행렬, Ψ를 대각 원소가 고유 분산, Ψi인 p × p 대각 행렬로 정의합니다. 그런 다음 우도 함수, f(L,Ψ)를 최대화하는 L과 Ψ의 값을 찾아야 합니다. 여기에는 먼저 Ψ의 값을 찾은 다음 L의 값을 찾는 2단계 절차가 포함됩니다.
Ψ의 초기 값을 간접적으로 지정할 수 있습니다. 인자 분석 - 옵션 하위 대화 상자에서 초기 공통성 추정치 사용에 공통성에 대한 초기 값이 포함되어 있는 열을 입력합니다. 그런 다음 Minitab에서 Ψ의 대각 원소를 (1 − 공통성)으로 계산합니다.
고정된 Ψ 값에 대해 f(L,Ψ)를 L에 대해 최대화합니다. 이 계산은 간단한 행렬 계산입니다. 그런 다음 L의 값이 f(L,Ψ)로 대체됩니다. 이제 f를 Ψ의 함수로 볼 수 있습니다. 이 함수는 간단히 다음과 같이 변환됩니다.
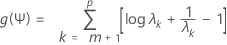
여기서 λ1 < λ2 < ... λp는 Ψ R- 1Ψ의 고유값입니다. 그런 다음 Newton-Raphson 절차를 사용하여 g(Ψ)를 최소화합니다. 이를 통해 Ψ의 추정치가 계산되어 우도 f(L,Ψ)로 대체됩니다. 그런 다음 우도가 L에 대해 다시 최대화됩니다. 그런 다음 새 g(Ψ) 값이 계산되며 이런 식으로 계속됩니다. 기본적으로 수렴에 도달하지 않을 경우 최대 25단계까지 반복이 계속됩니다. 25단계 후에도 알고리즘이 수렴하지 않을 경우 옵션 하위 대화 상자에서 기본 최대 반복 횟수를 변경할 수 있습니다.
다음 중 하나가 참인 경우 단계 n에서 수렴에 도달합니다.
- 특히 다음과 같은 경우, 연속적 단계 사이에 함수 g(Ψ)가 크게 달라지지 않습니다.
- | [ 단계 n의 g(Ψ)] − [단계 (n - 1)의 g(Ψ)] | < 10-6
- 특히 다음과 같은 경우 연속적 단계 사이에 고유 분산이 크게 달라지지 않습니다.
- | ln(단계 n의 Ψi) − ln(단계 n - 1의 Ψi) | < K2,
(모든 i = 1, ... , p에 대해), 여기서 Ψ의 i번째 대각 원소 Ψi는 변수 i에 해당하는 고유 분산입니다.
K2의 값은 옵션 하위 대화 상자의 수렴에 지정할 수 있습니다. 기본값은 0.005입니다.
각 반복에 대한 정보를 표시하려면 결과 하위 대화 상자에서 전체 및 MLE 반복를 선택합니다. 목표 함수, g(Ψ)의 값이 표시된 다음 ln(Ψi)의 최대값이 변경됩니다. 한 번 반복 시 g(Ψ)의 값이 감소하지 않을 경우 더 작은(1/2 크기) 단계가 실행됩니다. 1/2 크기의 단계는 g(Ψ)가 감소하거나 1/2 크기의 단계가 25번 실행될 때까지 계속됩니다. 1/2 크기의 단계 수가 표시됩니다. 25번의 1/2 크기 단계 후에도 g(Ψ)가 감소하지 않을 경우 알고리즘이 중단되고 메시지가 표시됩니다.
이차 도함수의 행렬이 g(Ψ)의 최소화에 사용됩니다. 이 행렬은 양의 무한대가 아닐 수도 있습니다. 양의 무한대가 아닌 경우 근사가 사용됩니다. Minitab에서 정확한 행렬을 사용하는 경우 결과에 별표가 표시됩니다.
g(Ψ) 함수를 최소화하는 경우 0이나 음수인 Ψ의 대각 원소 값을 찾을 수 있습니다. 이를 방지하기 위해 Minitab의 알고리즘에서는 Ψ의 대각 원소를 0에서 떨어뜨려 묶습니다 특히, 고유 분산 Ψi가 K2인 경우 K2로 설정됩니다. K2는 옵션 하위 대화 상자의 수렴에 설정된 값입니다.
알고리즘이 수렴하는 경우 고유 분산에 대해 최종 확인이 수행됩니다. 고유 분산이 K2보다 작은 경우 0으로 설정됩니다. 해당하는 공통성은 1과 같습니다. 이 결과는 Heywood 사례라고 하며 Minitab은 사용자에게 결과를 알려주기 위해 메시지를 표시합니다. 최대우도 인자 분석에 사용되는 것과 같은 최적화 알고리즘은 입력을 약간 변경하여 여러 대답을 제공할 수 있습니다. 예를 들어, 데이터 점 몇 개를 변경하거나 초기 공통성 추정치 사용에서 시작 값을 변경하거나 수렴에서 수렴 기준을 변경하는 경우 인자 분석 결과에 차이가 있을 수도 있습니다. 특히 해가 최대우도 표면의 비교적 평평한 위치에 있는 경우 사실입니다.
적재 회전
직교 회전은 인자 적재를 더 쉽게 해석할 수 있는 인자 적재의 직교 변환입니다. 회전된 적재에는 상관 또는 공분산 행렬, 잔차 행렬, 특정 분산, 공통성이 포함됩니다. 적재가 변경되기 때문에 각 인자 및 해당하는 비율에 의해 설명되는 분산이 변경됩니다.
회전은 축을 가능한 많은 점에 가깝게 배치하며 각 변수 그룹을 인자와 연관시킵니다. 그러나 경우에 따라 하나의 변수가 두 개 이상의 축에 가깝기 때문에 두 개 이상의 인자와 연관됩니다.
네 가지 회전 방법 중에서 선택할 수 있습니다.
- Equimax - 변수와 인자 내 적재 제곱의 분산을 최대화합니다.
- Varimax - 인자 내 적재 제곱의 분산을 최대화합니다. 이 방법은 적재 행렬의 열을 단순화하며 가장 널리 사용되는 회전 방법입니다. 이 방법에서는 해석을 쉽게 하기 위해 적재를 크거나 작게 만듭니다.
- Quartimax - 변수 내 적재 제곱의 분산을 최대화합니다. 이 방법은 적재 행렬의 행을 단순화합니다.
- γ가 있는 Orthomax - 모수 감마의 값(0-1)에 따라 위의 세 가지 방법을 절충하는 회전 방법입니다.
인자 분석 모형
인자 분석 모형은 다음과 같습니다.
X = μ + L F + e
설명: X는 측정값의 p x 1 벡터, μ는 평균의 p x 1 벡터, L은 적재의 p × m 행렬, F는 공통 인자의 m × 1 벡터, e는 잔차의 p × 1 벡터입니다. 여기서 p는 하나의 피실험자 또는 항목의 측정값 수를 나타내고 m은 공통 인자의 수를 나타냅니다. F 및 e는 서로 독립적인 것으로 간주되며 개별 F는 서로 독립적입니다. F와 e의 평균은 0, Cov(F) = I(단위 행렬), Cov(e) = Ψ(대각 행렬)입니다. F의 독립성을 가정할 경우 이 모형이 직교 인자 모형이 됩니다.
인자 분석 모형에서 데이터의 p × p 공분산 행렬, X는 다음과 같이 계산됩니다.
Cov(X) = L L' + Ψ
설명: L은 적재의 p × m 행렬이고 Ψ는 p × p 대각 행렬입니다. 제곱 적재의 합, L L'의 i번째 대각 원소는 i번째 공통성이라고 합니다. 공통성 값은 공통 인자의 설명되는 변동성의 백분율로 판단할 수 있습니다. Ψ의 i번째 대각 원소는 i번째 특정 분산 또는 고유성이라고 합니다. 특정 분산은 공통 인자에 의해 설명되지 않는 변동 부분입니다. 공통성 및/또는 특정 분산의 크기는 적합도를 평가하기 위해 사용할 수 있습니다.
적재
공식
주성분 방법이 사용되는 경우 추정된 인자 적재의 행렬, L은 다음과 같이 계산됩니다.
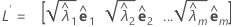
최대우도 방법이 사용되는 경우 인자 적재 행렬은 반복 과정을 통해 얻습니다.
표기법
| 용어 | 설명 |
|---|---|
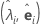 | 고유값-고유 벡터 쌍 |
공통성
공식
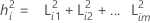
설명: i = 1, 2 ... p
표기법
| 용어 | 설명 |
|---|---|
| L | 인자 적재 행렬 |
분산
각 인자에 의해 설명되는 데이터의 변동성입니다. 주성분을 사용하여 인자를 추출하고 적재를 회전하지 않는 경우 분산은 고유값과 같습니다.
% Var
공식
상관 행렬이 사용되는 경우 j번째 인자에 의해 설명되는 분산의 비율은 다음과 같이 계산됩니다.
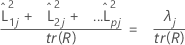
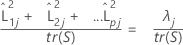
표기법
| 용어 | 설명 |
|---|---|
| L | 인자 적재 행렬 |
| λj | j번째 고유값 |
| tr(R) | 상관 행렬의 궤적 |
| tr(S) | 공분산 행렬의 궤적 |
계수
수식


R은 상관 관계 행렬입니다. 인자 분석을 할 행렬이 공분산 행렬인 경우 R은 공분산 행렬로 대체됩니다.
표기법
| 용어 | 설명 |
|---|---|
| L | 인자 적재 행렬 |
점수
공식
F = ZC
표기법
| 용어 | 설명 |
|---|---|
| F | 인자 점수의 행렬 |
| Z | 표준화된 데이터 |
| C | 인자 점수 계수의 행렬 |
