이 항목의 내용
설계 행렬
Minitab에서는 먼저 사용자가 지정한 요인 및 모형에서 설계 행렬을 만듭니다. 이 행렬의 열들이 모형의 항을 나타냅니다. 그런 다음 Minitab에서 상수 항, 블럭 및 고차 항에 대한 열을 추가하여 분석의 모형에 대한 설계 행렬을 완성합니다.
모든 계량형 요인이 포함된 설계
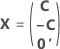
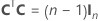
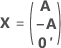
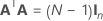
전체 설계 행렬에는 요인을 나타내는 열이 아닌 다른 열이 포함됩니다. 설계 행렬에는 상수 항에 대한 1의 열이 포함됩니다. 전체 설계 행렬에는 또한 모형의 제곱 또는 교호작용 항을 나타내는 열이 포함됩니다.
범주형 요인이 포함된 설계
범주형 요인이 포함된 설계의 경우 Minitab에서는 설계 행렬의 중앙점 행 하나를 유사 중앙점 2개로 바꿉니다. 설계에 범주형 요인이 하나만 있는 경우에는 유사 중앙점이 2개만 존재하며, 따라서 두 점 모두 설계에 포함됩니다.
설계에 범주형 요인이 3개 이상 있는 경우 Minitab에서는 반복 알고리즘을 사용하여 포함할 유사 중앙점 2개를 선택합니다. 알고리즘은 모형의 선형 효과에 대한 회귀 계수의 분산을 최소화하려고 합니다.
표기법
| 용어 | 설명 |
|---|---|
| C | 컨퍼런스 행렬 |
| 0' | 행렬에서 중앙점 런을 나타내는 0의 행 |
| In | n × n 단위 행렬 |
| A | 행이 N개, 열이 n개인 컨퍼런스 행렬의 부분 집합인 행렬, 여기서  |
| N | 컨퍼런스 행렬의 열 부분 집합에 있는 행 수 |
| n | 설계의 요인 수 |
계수
행렬 항에서 모형 내 계수의 벡터를 계산하는 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| X | 설계 행렬 |
| Y | 반응 벡터 |
Box-Cox 변환
Box-Cox 변환은 아래와 같이 잔차 제곱합을 최소화하는 람다 값을 선택합니다. 결과 변환은 λ ≠ 0일 때 Y λ, λ = 0일 때 ln(Y)입니다. λ < 0인 경우 Minitab에서는 변환되지 않은 반응의 순서를 유지하기 위해 변환된 반응에 −1을 곱합니다.
Minitab은 -2와 2 사이의 최적 값을 검색합니다. 이 구간을 벗어나는 값의 결과는 더 적합하지 않을 수 있습니다.
Y'가 데이터 Y의 변환인 일반적인 변환의 몇 가지 예는 다음과 같습니다.
| 람다(λ) 값 | 변환 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 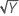 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
가중 회귀 분석
가중 최소 제곱법은 분산이 일정하지 않은 관측치를 처리하기 위한 방법입니다. 분산이 일정하지 않으면 관측치는 다음과 같은 경우 중 하나로 처리됩니다.
- 큰 분산에는 상대적으로 작은 가중치를 부여해야 합니다.
- 작은 분산에는 상대적으로 큰 가중치를 부여해야 합니다.
일반적으로 반응의 순수 오차 변동의 역이 가중치로 선택됩니다.
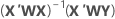
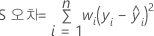
표기법
| 용어 | 설명 |
|---|---|
| X | 설계 행렬 |
| X' | 설계 행렬의 전치 |
| W | 대각선에 가중치가 있는 n x n 행렬 |
| Y | 반응 값의 벡터 |
| n | 관측치 수 |
| wi | i번째 관측치에 대한 가중치 |
| yi | i번째 관측치에 대한 반응 값 |
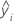 | i번째 관측치에 대한 적합치 |
