확정 선별 설계를 위한 이항 반응 분석 방법

기존 선형 모형을 일반화 선형 모형으로 확장하려면 지수 모임 분포와 연결 함수의 두 가지 부분이 필요합니다.

지수 모임

첫 부분에서는 선형 모형을 지수 모임이라는 큰 분포 모임의 구성원인 반응 변수로 확장합니다. 분포의 지수 모임에 속한 구성원은 관측된 반응에 대해 다음과 같은 일반적인 형식의 확률 분포 함수를 갖습니다.

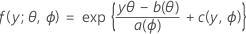
여기서 a(∙), b(∙) 및 c(∙)는 반응 변수의 분포에 종속됩니다. 모수 θ는 보통 표준 모수라고 하는 위치 모수이고, ϕ는 산포 모수라고 합니다. 함수 a(ϕ)는 일반적으로 a(ϕ)= ϕ/ ω 형태이고, 여기서 ω는 알려진 상수 또는 관측치에 따라 달라질 수도 있는 가중치입니다. (Minitab에서 가중치가 주어지면 함수 a(ϕ)가 적절히 조정됩니다.)

지수 모임의 구성원은 이산형 분포이거나 계량형 분포일 수 있습니다. 지수 모임의 구성원인 계량형 분포의 예는 정규 및 감마 분포입니다. 지수 모임의 구성원인 이산형 분포의 예는 이항 및 포아송 분포입니다. 아래 표에는 이러한 분포 특성들이 나와 있습니다.

분포	ϕ	b(θ)	a(φ)	c(y, ϕ)
정규 분포	σ2	θ2/2	φω
이항 분포	1		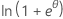φ/ω	-ln(y!)
포아송 분포	1	exp(θ)	φ/ω

연결 함수

두 번째 부분은 연결 함수입니다. 연결 함수는 i 번째 관측치의 반응 평균을 다음과 같은 형식으로 선형 예측 변수에 연결합니다.

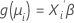
기존 선형 모형은 연결 함수가 항등원 함수인 이 일반 공식의 특별한 경우입니다.

두 번째 부분에서 선택하는 연결 함수는 첫 부분의 지수 모임의 특정 분포에 따라 결정됩니다. 특히 지수 모임의 각 분포에는 정규 연결 함수라는 특수 연결 함수가 있습니다. 이 연결 함수는 θ가 정규 모수인 g (μ_i) = X_i'β= θ 방정식을 충족합니다. 정규 연결 함수의 결과는 몇 가지 바람직한 모형의 통계적 속성입니다. 적합도 통계량은 다른 연결 함수를 사용하여 적합치를 비교하는 데 사용할 수 있습니다. 일부 연결 함수는 경험적인 이유로 또는 원칙에 있어 특별한 의미를 가지고 있기 때문에 사용할 수도 있습니다. 예를 들어, 로짓연결함수의 장점은 승산비의 추정치를 제공한다는 것입니다. 또 다른 예는 노밋 연결 함수에서는 이원 범주로 분류된 정규 분포를 따르는 기본 변수가 있다고 가정한다는 것입니다.

Minitab은 세 가지 연결 함수를 제공합니다. 서로 다른 연결 함수를 사용하여 다양한 데이터에 충분히 적합한 모형을 찾을 수 있습니다. 연결 함수는 로짓, 노밋(프로빗) 및 곰핏(보 로그-로그)입니다. 이 연결 함수들은 누적 로지스틱 분포 함수의 역함수(로짓), 표준 누적 정규 분포 함수의 역함수(노밋), 그리고 Gompertz 분포 함수의 역함수(곰핏)입니다. 로짓은 이항 분포 모형에 대한 정규 연결 함수이므로, 로짓이 기본 연결 함수입니다.

모형	이름	연결 함수, g(μi)
이항 분포	로짓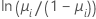
이항 분포	노밋(프로빗)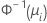
이항 분포	곰핏(보 로그-로그)

표기법

용어	설명
μi	i 번째 행의 평균 반응
g(μi)	연결 함수
X	예측 변수의 벡터
β	예측 변수와 연관된 계수의 벡터
	정규 분포의 역 누적분포함수

데이터 집합의 단일 요인/공변량 값 집합에 대해 설명합니다. Minitab에서는 각 요인/공변량 패턴에 대한 사건 확률, 잔차 및 기타 진단 측도를 계산합니다.

예를 들어 데이터 집합에 성별 및 인종 요인과 나이 공변량이 포함되어 있는 경우, 이런 예측 변수의 조합에는 피실험자 수만큼 많은 공분산 패턴이 포함될 수 있습니다. 데이터 집합에 각각 2개 수준에서 코드화된 인종과 성별 요인만 포함되어 있는 경우, 가능한 요인/공변량 패턴은 4개뿐입니다. 데이터를 빈도나 성공, 시행 또는 실패 횟수로 입력할 경우 각 행에 요인/공변량 패턴이 하나씩 포함됩니다.

Minitab에서는 먼저 사용자가 지정한 요인 및 모형에서 설계 행렬을 만듭니다. 이 행렬의 열들이 모형의 항을 나타냅니다. 그런 다음 Minitab에서 상수 항, 블럭 및 고차 항에 대한 열을 추가하여 분석의 모형에 대한 설계 행렬을 완성합니다.

모든 계량형 요인이 포함된 설계

설계 행렬의 형태는 행의 개수가 요인 수와 같은 컨퍼런스 행렬이 존재하는지 여부에 따라 다릅니다. 이 기준이 참인 경우 요인을 나타내는 설계 행렬의 열은 다음과 같은 형태입니다.

여기서 C는 다음과 같은 특성을 충족하는 {-1, 0, 1} 원소가 있는 n× n 컨퍼런스 행렬입니다.

올바른 크기의 컨퍼런스 행렬이 존재하지 않는 경우 요인을 나타내는 열은 더 큰 컨퍼런스 행렬의 부분 집합입니다.

여기서 A는 다음과 같은 특성을 충족하는 {-1, 0, 1} 원소가 있는 N× n 행렬입니다.

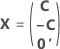
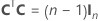
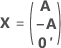
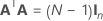
전체 설계 행렬에는 요인을 나타내는 열이 아닌 다른 열이 포함됩니다. 설계 행렬에는 상수 항에 대한 1의 열이 포함됩니다. 전체 설계 행렬에는 또한 모형의 제곱 또는 교호작용 항을 나타내는 열이 포함됩니다.

범주형 요인이 포함된 설계

범주형 요인이 포함된 설계의 경우 Minitab에서는 설계 행렬의 중앙점 행 하나를 유사 중앙점 2개로 바꿉니다. 설계에 범주형 요인이 하나만 있는 경우에는 유사 중앙점이 2개만 존재하며, 따라서 두 점 모두 설계에 포함됩니다.

설계에 범주형 요인이 3개 이상 있는 경우 Minitab에서는 반복 알고리즘을 사용하여 포함할 유사 중앙점 2개를 선택합니다. 알고리즘은 모형의 선형 효과에 대한 회귀 계수의 분산을 최소화하려고 합니다.

표기법

용어	설명
C	컨퍼런스 행렬
0'	행렬에서 중앙점 런을 나타내는 0의 행
In	n × n 단위 행렬
A	행이 N개, 열이 n개인 컨퍼런스 행렬의 부분 집합인 행렬, 여기서
N	컨퍼런스 행렬의 열 부분 집합에 있는 행 수
n	설계의 요인 수