적합치
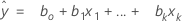
표기법
| 용어 | 설명 |
|---|---|
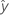 | 적합치 |
| xk | k번째 항. 각 항은 단일 예측 변수, 다항식 항 또는 교호작용 항입니다. |
| bk | k번째 회귀 계수의 추정치 |
적합치의 표준 오차(SE 적합치)
예측 변수가 하나인 회귀 모형 적합치의 표준 오차는 다음과 같습니다.

예측 변수가 두 개 이상인 회귀 모형 적합치의 표준 오차는 다음과 같습니다.

가중치 가중 회귀를 위해 방정식에 가중치 행렬을 포함합니다.

데이터에 테스트 데이터 집합 또는 K-fold 교차 유효성 검사가 있는 경우 수식은 동일합니다. 의 가치는 s도 2는 학습 데이터에서 나온 것입니다. 설계 행렬과 웨이트 매트릭스도 학습 데이터에서 사용됩니다.
표기법
| 용어 | 설명 |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | i번째 predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x'0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
잔차
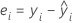
표기법
| 용어 | 설명 |
|---|---|
| yi | i번째 관측 반응치 |
 | 반응에 대한 i번째 적합치 |
표준화 잔차
표준화 잔차는 "내적 스튜던트화 잔차"라고도 합니다.
공식

표기법
| 용어 | 설명 |
|---|---|
| ei | i번째 잔차 |
| hi | X(X'X)–1X'의 i번째 대각 원소 |
| s 2 | 평균 제곱 오차 |
| X | 설계 행렬 |
| X' | 설계 행렬의 전치 |
외적 스튜던트화 잔차
외적 스튜던트화 잔차. 공식은 다음과 같습니다.
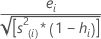
이 공식은 또한 다음과 같이 표시됩니다.

i번째 관측치를 추정하는 모형에서 데이터 집합의 i번째 관측치가 제외됩니다. 따라서 i번째 관측치는 추정치에 영향을 미치지 않습니다. 각 외적 스튜던트화 잔차에는 자유도가 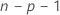 인 t-분포가 있습니다.
인 t-분포가 있습니다.
표기법
| 용어 | 설명 |
|---|---|
| ei | i번째 잔차 |
| s(i)2 | i번째 관측치를 포함하지 않고 계산한 평균 제곱 오차 |
| hi | X(X'X)–1X'의 i번째 대각 원소 |
| n | 관측치 수 |
| p | 항 수, 상수 포함 |
| SSE | 오차의 제곱합 |
신뢰 구간
주어진 예측 변수 값의 집합에 대해 추정된 평균 반응 값이 포함될 것으로 예상되는 범위. 이 구간은 신뢰 수준과 적합치의 표준 오차로부터 계산되는 하한과 상한으로 정의됩니다.

설명:

표기법
| 용어 | 설명 |
|---|---|
| α | 선택된 알파 값 |
| n | 관측치 수 |
| p | 모수의 수 |
| s2 | 평균 제곱 오차 |
| s2{b} | 계수의 분산-공분산 행렬 |
예측 구간
새 관측치의 예측 반응 값이 포함될 것으로 예상되는 범위. 이 구간은 신뢰 수준과 예측치의 표준 오차를 사용하여 계산되는 하한과 상한으로 정의됩니다. 평균 반응에 대한 단일 반응을 예측하는 데 불확실성이 추가되므로 예측 구간은 항상 신뢰 구간보다 넓습니다.
공식은 다음과 같습니다. 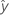 0+ t(1 -α /2; n - p) s(pred)
0+ t(1 -α /2; n - p) s(pred)
표기법
| 용어 | 설명 |
|---|---|
| α | 선택된 알파 값 |
| n | 관측치 수 |
| p | 예측 변수의 수 |
| s (predi | 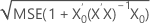 |
