원하는 방법 또는 공식을 선택하십시오.
심플렉스 중심 설계
성분이 q개인 혼합물에 대한 심플렉스 중심 설계는 2**q - 1개의 점으로 구성됩니다. 설계점은 다음과 같습니다.
- 하나의 성분 xi = 1이고 나머지는 0인 모든 점(x1, x2, ..., xq). 이 점들은 꼭지점이라고 합니다.
- 하나의 성분, xi = 1/2, 다른 성분, xj = 1/2이고 나머지는 0인 모든 점.
- 하나의 성분 xi = 1/3, 다른 성분 xj = 1/3, 또 다른 성분 xk = 1/3이고 나머지는 0인 모든 점.
- 모든 성분이 1/q일 때까지 이 패턴이 계속됩니다. 모든 성분이 같은 이 마지막 점을 설계의 중심이라고 합니다.
심플렉스 격자 설계
심플렉스 격자 설계에는 격자도가 m인 q개의 성분(변수)이 있습니다. 차수는 1에서 10까지입니다. Minitab에서는 다음과 같은 설계를 생성할 수 있습니다.
| 격자도(m) | 성분 수(q) |
|---|---|
| 1 | 2 - 20 |
| 2 | 2 - 20 |
| 3 | 2 - 17 |
| 4 | 2 - 11 |
| 5 | 2 - 8 |
| 6 | 2 - 7 |
| 7 | 2 - 6 |
| 8 | 2 - 5 |
| 9 | 2 - 5 |
| 10 | 2 - 5 |
꼭지점 설계
Minitab에서는 XVERT 알고리즘을 사용하여 제약된 설계 공간의 꼭지점을 생성한 다음 Piepel의 CONAEV 알고리즘을 사용하여 지정된 차수까지 중심을 계산합니다. 자세한 내용은 Cornell1 및 St. John2에서 확인하십시오.
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
- R.C. St. John (1984). "Experiments With Mixtures in Conditioning and Ridge Regression," Journal of Quality Technology 16, pp.81-96.
실험 유형
Minitab에서는 세 가지 유형의 실험에서 데이터를 분석할 수 있습니다.
| 유형 | 반응에 영향을 미치는 요소 |
| 혼합물 | 성분의 상대적인 비율만. |
| 혼합물-공정 변수 | 성분 및 공정 변수. 공정 변수는 혼합물의 부분이 아니지만 반응에 영향을 미칠 수 있는 실험 요인입니다. |
| 혼합물-양 | 각 성분의 상대적인 비율 및 혼합물의 총계. |
증대된 설계에서의 축 점 배치
Minitab에서는 다음과 같이 설계를 증대하거나 설계에 점을 추가합니다. 각 점은 설계의 꼭지점과 중앙점 사이의 중간 지점에 추가됩니다.
설계를 증대하면 가장자리에 의존하는 대신 설계 내부의 반응에 대한 정보를 얻을 수 있습니다.
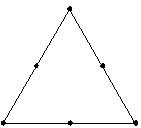
증대 전
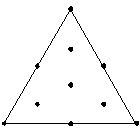
증대 후
성분 단위 변환
Minitab에서 양, 비율 및 유사 성분 단위로 설계를 생성하고 데이터를 분석할 수 있습니다.
데이터를 양에서 비율 단위로 변환하기 위한 공식은 다음과 같습니다.
- 비율 = 양 / 총계
총계 = 1이면 비율 단위 = 양 단위입니다.
데이터를 비율에서 유사 성분 단위로 변환하기 위한 공식은 다음과 같습니다.
- 유사 성분 = (비율 - 낮음) / (1 - 하한의 합)
- 비율 = 유사 성분 * (1 - 하한의 합) + 하한
모든 하한 = 0이면 유사 성분 단위 = 비율 단위입니다.
모형 항
혼합물 설계에는 여러 유형의 모형이 포함됩니다. 항 및 항의 표현 방법은 다음과 같습니다.
| 모형 | 항 |
| 선형 | A B C |
| 2차 | 선형 + AB AC BC |
| 특수 3차 | 2차 + ABC |
| 완전 3차 | 특수 3차 + AB(A-B) AC(A-C) BC(B-C) |
| 특수 4차 | 2차 + AABC ABBC ABCC |
| 완전 4차 | 특수 2차 + AB(A-B) AC(A-C) BC(B-C) AB(A-B)2 AC(A-C)2 BC(B-C)2 |
혼합물 모형에는 상수 항이 없습니다. 역 항에는 1/A, 1/B, 1/C 등이 포함됩니다.
