원하는 방법 또는 공식을 선택하십시오.
계수
Minitab에서는 최소 제곱 추정 방법을 사용하여 계수를 계산합니다.
행렬 항에서 계수의 최소 제곱 추정치는 다음과 같습니다.
b = (X'X)-1X'y
고차 모형의 계수에 대한 자세한 내용은 Cornell1을 참조하십시오.
표기법
| 용어 | 설명 |
|---|---|
| X | 설계 행렬 |
| y | 반응 열 |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
계수 표준 오차(SE Coef)
단순 선형 회귀의 경우 계수 표준 오차는 다음과 같습니다.
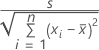
다중 회귀 분석의 계수 표준 오차는 다음 행렬의 대각선 요소들의 제곱근입니다.
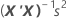
표기법
| 용어 | 설명 |
|---|---|
| xi | t번째 예측 변수 값 |
 | 예측 변수의 평균 |
| X | 설계 행렬 |
| X' | 설계 행렬의 전치 |
| s2 | 평균 제곱 오차 |
t-값
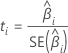
표기법
| 용어 | 설명 |
|---|---|
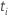 | 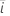 계수에 대한 검정 통계량 계수에 대한 검정 통계량 |
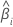 | 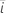 추정된 계수 추정된 계수 |
 | 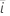 추정된 계수의 표준 오차 추정된 계수의 표준 오차 |
p-값 - 계수 표
회귀 계수가 0이라는 귀무 가설에 대한 양측 p-값은 다음과 같습니다.
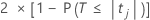
자유도는 다음과 같이 오차에 대한 자유도입니다.
n – p
표기법
| 용어 | 설명 |
|---|---|
 | 자유도가 오차에 대한 자유도와 같은 t 분포의 누적분포함수. |
| tj | j번째 계수에 대한 t 통계량. |
| n | 데이터 집합의 관측치 수. |
| p | 항에 대한 자유도의 합. |
분산 팽창 인수(VIF)
VIF는 각 예측 변수를 나머지 예측 변수에 회귀하고 R2 값을 참고하여 얻을 수 있습니다.
공식
예측 변수가 xj인 경우 VIF는 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| R2( xj) | 반응 변수가 xj이고 예측 변수가 모형의 나머지 항인 결정 계수 |
