잔차 히스토그램
잔차 히스토그램은 모든 관측치에 대한 잔차의 분포를 보여줍니다.
해석
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 한 쪽 방향의 긴 꼬리 | 왜도 |
| 다른 막대들과 멀리 떨어져 있는 막대 | 특이치 |
히스토그램 모양은 데이터를 그룹으로 나누는 데 사용된 구간 수에 따라 다르므로, 히스토그램을 사용하여 잔차의 정규성을 평가하지 마십시오.
히스토그램은 데이터 점의 수가 약 20개 이상일 때 가장 효과적입니다. 표본이 너무 작으면 왜도 또는 특이치를 높은 신뢰도로 보여주기에 충분한 데이터 점이 히스토그램의 각 막대에 포함되지 않습니다.
잔차 대 적합치
잔차 대 적합치 그림은 y-축에 잔차, x-축에 적합치를 표시합니다.
해석
잔차가 랜덤하게 분포되어 있고 잔차의 분산이 일정하다는 가정을 확인하려면 잔차 대 적합치 그림을 사용하십시오. 이상적으로는 점들이 식별 가능한 패턴 없이 0의 양쪽에 랜덤하게 분포해야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 적합치에 대해 잔차가 부채꼴 모양으로 흩어져 있거나 고르지 않게 퍼져 있음 | 일정하지 않은 분산 |
| 곡선 | 고차 항 누락 |
| 한 점이 0에서 멀리 떨어져 있음 | 특이치 |
| 다른 점에서 x 방향으로 멀리 떨어져 있는 점 | 영향력 있는 점 |

특이치가 있는 그래프
점 중 하나가 나머지 모든 점보다 훨씬 더 큽니다. 따라서 그 점이 특이치입니다. 특이치가 너무 많으면 모형이 적절하지 않을 수 있습니다. 특이치의 원인을 식별해야 합니다. 모든 데이터 입력 또는 측정 오류를 수정하십시오. 비정상적인 일회성 사건과 연관된 데이터 값을 삭제해 보십시오(특수 원인). 그런 다음 분석을 반복하십시오.
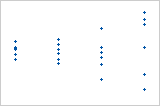
일정하지 않은 분산이 있는 그림
잔차의 분산이 적합치에 따라 증가합니다. 적합치가 증가하면 잔차 간의 산포가 더 넓어집니다. 이 패턴은 잔차의 분산이 동일하지(일정하지) 않다는 것을 나타냅니다.
- 관측치가 측정 오류 또는 데이터 입력 오류인지 확인하십시오.
- 이 관측치 없이 분석을 수행하여 결과에 어떤 영향을 미치는지 살펴보십시오.
잔차 대 순서
잔차 대 순서 그림은 잔차를 데이터가 수집된 순서대로 표시합니다.
해석
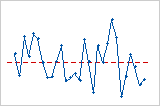
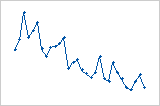
추세
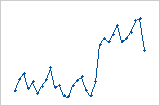
교대조
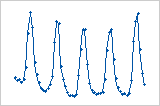
주기
잔차 대 변수
잔차 대 변수 그림은 잔차 대 다른 변수를 표시합니다. 변수가 이미 모형에 포함되어 있을 수 있습니다. 또는 변수가 모형에 포함되어 있지 않을 수도 있지만 반응 변수에 영향을 미칠 것으로 예상됩니다.
해석
변수가 이미 모형에 포함되어 있는 경우 이 그림을 사용하여 변수의 고차 항을 추가해야 할지 여부를 결정합니다. 변수가 모형에 아직 포함되지 않은 경우에는 이 그림을 사용하여 변수가 체계적인 방식으로 반응에 영향을 미치는지 여부를 확인합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 잔차의 패턴 | 변수가 체계적으로 반응에 영향을 미칩니다. 모형에 변수가 없는 경우에는 해당 변수에 대한 항을 포함하고 모형을 다시 적합시킵니다. |
| 점의 곡면성 | 변수의 고차 항을 모형에 포함해야 합니다. 예를 들어, 곡선이 있는 패턴은 제곱 항을 추가해야 한다는 것을 의미합니다. |
