이 항목의 내용
지수 모임 및 연결 함수
기존 선형 모형을 일반화 선형 모형으로 확장하려면 지수 모임 분포와 연결 함수의 두 가지 부분이 필요합니다.
지수 모임
첫 부분에서는 선형 모형을 지수 모임이라는 큰 분포 모임의 구성원인 반응 변수로 확장합니다. 분포의 지수 모임에 속한 구성원은 관측된 반응에 대해 다음과 같은 일반적인 형식의 확률 분포 함수를 갖습니다.
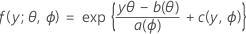
여기서 a(∙), b(∙) 및 c(∙)는 반응 변수의 분포에 종속됩니다. 모수 θ는 보통 표준 모수라고 하는 위치 모수이고, ϕ는 산포 모수라고 합니다. 함수 a(ϕ)는 일반적으로 a(ϕ)= ϕ/ ω 형태이고, 여기서 ω는 알려진 상수 또는 관측치에 따라 달라질 수도 있는 가중치입니다. (Minitab에서 가중치가 주어지면 함수 a(ϕ)가 적절히 조정됩니다.)
지수 모임의 구성원은 이산형 분포이거나 계량형 분포일 수 있습니다. 지수 모임의 구성원인 계량형 분포의 예는 정규 및 감마 분포입니다. 지수 모임의 구성원인 이산형 분포의 예는 이항 및 포아송 분포입니다. 아래 표에는 이러한 분포 특성들이 나와 있습니다.
| 분포 | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| 정규 분포 | σ2 | θ2/2 | φω |  |
| 이항 분포 | 1 | 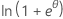 |
φ/ω | -ln(y!) |
| 포아송 분포 | 1 | exp(θ) | φ/ω |  |
연결 함수
두 번째 부분은 연결 함수입니다. 연결 함수는 i 번째 관측치의 반응 평균을 다음과 같은 형식으로 선형 예측 변수에 연결합니다.
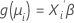
기존 선형 모형은 연결 함수가 항등원 함수인 이 일반 공식의 특별한 경우입니다.
두 번째 부분에서 선택하는 연결 함수는 첫 부분의 지수 모임의 특정 분포에 따라 결정됩니다. 특히 지수 모임의 각 분포에는 정규 연결 함수라는 특수 연결 함수가 있습니다. 이 연결 함수는 θ가 정규 모수인 g (μi) = Xi'β= θ 방정식을 충족합니다. 정규 연결 함수의 결과는 몇 가지 바람직한 모형의 통계적 속성입니다. 적합도 통계량은 다른 연결 함수를 사용하여 적합치를 비교하는 데 사용할 수 있습니다. 일부 연결 함수는 경험적인 이유로 또는 원칙에 있어 특별한 의미를 가지고 있기 때문에 사용할 수도 있습니다. 예를 들어, 로짓연결함수의 장점은 승산비의 추정치를 제공한다는 것입니다. 또 다른 예는 노밋 연결 함수에서는 이원 범주로 분류된 정규 분포를 따르는 기본 변수가 있다고 가정한다는 것입니다.
Minitab은 세 가지 연결 함수를 제공합니다. 서로 다른 연결 함수를 사용하여 다양한 데이터에 충분히 적합한 모형을 찾을 수 있습니다. 연결 함수는 로짓, 노밋(프로빗) 및 곰핏(보 로그-로그)입니다. 이 연결 함수들은 누적 로지스틱 분포 함수의 역함수(로짓), 표준 누적 정규 분포 함수의 역함수(노밋), 그리고 Gompertz 분포 함수의 역함수(곰핏)입니다. 로짓은 이항 분포 모형에 대한 정규 연결 함수이므로, 로짓이 기본 연결 함수입니다.
| 모형 | 이름 | 연결 함수, g(μi) |
| 이항 분포 | 로짓 | 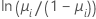 |
| 이항 분포 | 노밋(프로빗) | 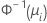 |
| 이항 분포 | 곰핏(보 로그-로그) |  |
표기법
| 용어 | 설명 |
|---|---|
| μi | i 번째 행의 평균 반응 |
| g(μi) | 연결 함수 |
| X | 예측 변수의 벡터 |
| β | 예측 변수와 연관된 계수의 벡터 |
 | 정규 분포의 역 누적분포함수 |
요인/공변량 패턴
데이터 집합의 단일 요인/공변량 값 집합에 대해 설명합니다. Minitab에서는 각 요인/공변량 패턴에 대한 사건 확률, 잔차 및 기타 진단 측도를 계산합니다.
예를 들어 데이터 집합에 성별 및 인종 요인과 나이 공변량이 포함되어 있는 경우, 이런 예측 변수의 조합에는 피실험자 수만큼 많은 공분산 패턴이 포함될 수 있습니다. 데이터 집합에 각각 2개 수준에서 코드화된 인종과 성별 요인만 포함되어 있는 경우, 가능한 요인/공변량 패턴은 4개뿐입니다. 데이터를 빈도나 성공, 시행 또는 실패 횟수로 입력할 경우 각 행에 요인/공변량 패턴이 하나씩 포함됩니다.
설계 행렬
일반 선형 모형(GLM)의 경우 회귀 분석을 사용하여 사용자가 지정한 모형을 적합하는 데 Minitab에서는 이와 동일한 방법을 설계 행렬에 사용합니다. Minitab에서는 먼저 사용자가 지정한 요인 및 모형에서 설계 행렬을 만듭니다. X라고 하는 이 행렬의 행들이 모형의 항을 나타냅니다.
- 상수
- 공변량
- 블럭
- 요인
- 교호작용
- 상수
- 공변량
- 계량형 요인
블럭의 경우 열의 수가 블럭의 수보다 하나 적습니다.
2-수준 설계의 범주형 요인 및 교호작용
2-수준 설계에서 범주형 요인에 대한 항은 하나의 열을 가집니다. 모든 교호작용도 하나의 열을 가집니다.
일반 요인 설계의 범주형 요인
| A 수준 | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | -1 | -1 | -1 |
일반 요인 설계의 교호작용
교호작용 항에 대한 열을 계산하려면 교호작용의 요인에 해당하는 모든 열을 곱하십시오. 예를 들어, 요인 A의 수준이 6개이고, C의 수준이 3개이고, D의 수준이 4개라고 가정합니다. 이 경우 A * C * D 항에는 5 x 2 x 3 = 30개의 열이 있습니다. 수준을 구하려면 A의 각 열과 C의 각 열, D의 각 열을 곱하십시오.
분할구 설계의 주구 열
참고
Minitab에서는 이항 반응이 있는 분할구 설계를 분석하지 않습니다.
분할구 설계의 경우 Minitab에는 두 버전의 설계 행렬을 사용합니다. 한 버전은 2-수준 요인 설계에 사용되는 것과 같은 행렬입니다. 다른 행렬에는 주구를 나타내는 열의 블럭이 포함됩니다. 예를 들어, 주구 오차 항을 계산할 때는 설계 행렬의 이 두 번째 버전을 사용합니다. 주구에 대한 열은 변경하기 어려운 요인 및 변경하기 어려운 요인만 포함된 교호작용에 대한 열을 따릅니다.
