요인 설계를 위한 이항 반응 분석의 분산 분석 방법 및 공식

이탈도는 현재 모형과 전체 모형의 불일치를 측정합니다. 전체 모형은 관측치당 하나씩 총 n개의 모수가 있는 모형입니다. 전체 모형은 로그 우도 함수를 극대화합니다. 전체 모형은 모수가 n개 미만인 모형의 비교점이 됩니다. 전체 모형에 비교할 때는 척도화된 이탈도를 사용합니다.

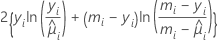
이탈도 표는 ϕ이 알려져 있다고 가정하는 다음과 같은 일반적인 결과를 근거로 작성됩니다. D_I가 최초 모형과 관련된 이탈도이고 D_S가 최초 모형에 있는 항의 부분 집합과 관련된 이탈도인 경우, 일부 정규성 조건에 따라 다음과 같은 관계가 존재합니다.

이탈도의 차이는 자유도가 d인 카이-제곱 분포로 비동시적으로 분포됩니다. 이런 통계량은 수정(유형 III) 분석과 순차(유형 I) 분석에 대해 계산됩니다. 이탈도 표의 수정 이탈도와 카이-제곱 통계량은 같습니다. 수정 평균 이탈도는 수정 이탈도 나누기 자유도입니다.

순차 분석의 경우 출력은 예측 변수가 모형에 들어오는 순서에 따라 다릅니다. 순차 이탈도는 모형에 이미 있는 예측 변수가 제공된 경우 예측 변수가 설명하는 이탈도의 고유한 부분입니다. X1, X2, X3라는 3개의 예측 변수가 포함된 모형이 있는 경우, X3에 대한 순차 이탈도는 X1과 X2가 이미 모형에 있다는 전제 하에 X3가 잔여 이탈도를 얼마나 설명하는지 보여줍니다. 다른 순차 이탈도를 얻으려면 예측 변수를 입력하는 회귀 분석 절차를 다른 순서로 반복하십시오.

정규 분포를 따르는 반응의 경우처럼 ϕ를 알 수 없는 경우, 일부 규칙성 조건에서 관계가 다음과 같이 바뀝니다.

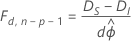
여기서 이탈도의 차이는 분자의 자유도가 d이고 분모의 자유도가 n − p인 F 분포로 비동시적으로 분포됩니다. 산포 모수를 추정하려면 최초 모형을 사용하십시오.

표기법

용어	설명
yi	i 번째 행의 사건 수
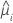	i 번째 행의 추정 평균 반응
mi	i 번째 행의 시행 횟수
Lf	전체 모형의 로그 우도
Lc	전체 모형 항의 부분 집합이 있는 모형의 로그 우도
d	자유도는 비교할 모형에 있는 모수 수의 차이입니다.
ϕ	이항 모형의 경우 1이라고 알려진 산포 모수
n	데이터의 행 수
p	최초 모형의 회귀 자유도

수정 평균 이탈도를 계산하는 데 필요한 반응 데이터와 관련된 독립적인 정보 수를 나타냅니다. 모형의 각 성분에 대한 자유도는 다음과 같습니다.

표기법

용어	설명
p	예측 변수의 자유도 합. 예측 변수에는 상수가 포함되지 않습니다.
n	설계의 행 수
q	범주형 예측 변수의 수준 수
b	블럭 수
a	요인 A의 수준 수
b	요인 B의 수준 수

로그 우도 함수는 평균에 대해 모수화됩니다. 함수의 일반적인 형식은 다음과 같습니다.

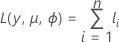
개별 기여의 일반적인 형식은 다음과 같습니다.

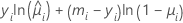
표기법

용어	설명
yi	i 번째 행의 사건 수
mi	i 번째 행의 시행 횟수
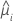	i 번째 행의 추정 평균 반응

귀무 가설을 기각하거나 받아들이는 가설 검정에서 사용됩니다. p-값은 귀무 가설이 참인 경우 최소한 실제로 계산된 값만큼 극단적인 검정 통계량을 얻을 확률입니다. 일반적으로 사용되는 p-값에 대한 컷오프 값은 0.05입니다. 예를 들어, 검정 통계량의 계산된 p-값이 0.05보다 작으면 귀무 가설을 기각합니다.