이탈도 R-제곱
이탈도 R2은 일반적으로 모형이 설명하는 반응 변수 내 총 이탈도의 비율로 간주됩니다.
해석
이탈도 R2이 클수록 모형이 데이터를 더 잘 적합시킵니다. 이탈도 R2은 항상 0%에서 100% 사이입니다.
모형에 항을 추가하면 이탈도 R2은 항상 증가합니다. 예를 들어, 최량 항이 5개인 모형은 최량 항이 4개인 모형보다 항상 R2 값이 큽니다. 따라서 이탈도 R2은 같은 크기의 모형을 비교할 때 가장 유용합니다.
적합도 통계량은 모형이 데이터를 얼마나 잘 적합시키는 지에 대한 하나의 측도에 지나지 않습니다. 모형에 바람직한 값이 있더라도 해당 모형이 데이터를 충족하는지 확인하려면 잔차 그림 및 적합도 검정을 확인해야 합니다.
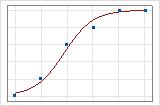
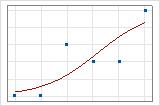
적합선 그림을 사용하여 서로 다른 이탈도 R2 값을 그래픽으로 표시할 수 있습니다. 첫 번째 그림은 반응의 이탈도를 약 96% 설명하는 모형을 나타냅니다. 두 번째 그림은 반응의 이탈도를 약 60% 설명하는 모형을 나타냅니다. 모형이 이탈도를 더 많이 설명할수록 데이터 점이 곡선에 더 가깝게 표시됩니다. 이론적으로는 모형이 이탈도의 100%를 설명할 수 있는 경우 적합치가 항상 관측치와 같고 모든 데이터 점이 곡선 위에 있습니다.
데이터 배열은 이탈도 R2 값에 영향을 미칩니다. 일반적으로 행당 시행 횟수가 여러 번인 데이터에 대한 이탈도 R2이 행당 시행 횟수가 한 번인 데이터보다 큽니다. 이탈도 R2 값은 동일한 데이터 형식을 사용하는 모형 간에만 유사합니다. 자세한 내용은 이항 로지스틱 회귀 분석에서 데이터 형식이 적합도에 미치는 영향에서 확인하십시오.
이탈도 R-제곱(수정)
수정된 이탈도 R2은 관측치 수에 상대적인 모형의 예측 변수 개수에 따라 수정되고 모형에 의해 설명되는 반응 내 이탈도의 비율입니다.
해석
항 수가 다른 여러 모형을 비교하려면 수정 이탈도 R2을 사용하십시오. 모형에 항을 추가하면 이탈도 R2은 항상 증가합니다. 수정 이탈도 R2 값은 모형의 항 수에 통합되어 올바른 모형을 선택하는 데 유용합니다.
| 단계 | 감자 % | 냉각 비율 | 조리 온도 | 이탈도 R2 | 수정 이탈도 R2 | P-값 |
|---|---|---|---|---|---|---|
| 1 | X | 52% | 51% | 0.000 | ||
| 2 | X | X | 63% | 62% | 0.000 | |
| 3 | X | X | X | 65% | 62% | 0.000 |
첫 번째 단계에서 통계적으로 유의한 회귀 모형이 생성됩니다. 모형에 냉각 속도를 추가하는 두 번째 단계에는 수정 이탈도 R2가 증가하므로, 냉각 속도가 모형을 개선함을 나타냅니다. 모형에 조리 온도를 추가하는 세 번째 단계에서는 이탈도 R2가 증가하지만 수정 이탈도 R2는 증가하지 않습니다. 이 결과는 조리 온도가 모형을 개선하지 않는다는 것을 나타냅니다. 이 결과를 토대로 모형에서 조리 온도를 제거하는 것을 고려해 볼 수 있습니다.
데이터 배열은 수정 이탈도 R2 값에 영향을 미칩니다. 같은 데이터의 경우 일반적으로 행당 시행 횟수가 여러 번인 데이터에 대한 이탈도 R2이 행당 시행 횟수가 한 번인 데이터보다 큽니다. 데이터 형식이 같은 모형의 적합치를 비교하려면 수정 이탈도 R2만을 사용하십시오. 자세히 알려면 이항 로지스틱 회귀 분석에서 데이터 형식이 적합도에 미치는 영향(으)로 이동하십시오.
AIC, AICc 및 BIC
AIC(Akaike Information Criterion), 교정된 AICc(Akaike Information Criterion) 및 BIC(Bayesian Information Criterion)는 모형의 적합치와 항 수를 설명하는 모형의 상대적 품질 측도입니다.
해석
- AICc 및 AIC
- 표본 크기가 모형의 모수에 비해 작은 경우 AICc가 AIC보다 잘 수행됩니다. 표본 크기가 상대적으로 작으면 AIC가 모수가 너무 많은 모형의 경우 작은 경향이 있으므로 AICc가 더 잘 수행됩니다. 일반적으로, 표본 크기가 모형의 모수에 비해 충분히 큰 경우 비슷한 결과를 제공합니다.
- AICc 및 BIC
- AICc와 BIC 모두 모형의 우도를 평가한 다음 모형에 항을 추가하는 데 대한 벌칙을 적용합니다. 벌칙은 모형을 표본 데이터에 과다 적합하는 경향을 줄입니다. 이에 따라 일반적으로 더 잘 수행되는 모형이 생성됩니다.
