Tukey의 방법은 분산 분석에서 모임 오류율을 일정한 수준으로 유지하면서 요인 수준 평균 간의 모든 쌍 차이에 대한 신뢰 구간을 만드는 데 사용됩니다. 다중 비교에서 제1종 오류가 발생할 확률이 단일 비교의 오류율보다 크기 때문에 다중 비교를 할 경우에는 모임 오류율을 고려해야 합니다. 이와 같이 더 높은 오류율을 처리하기 위해 Tukey의 방법에서는 개별 구간의 신뢰 수준을 조정하여 그 결과 동시 신뢰 수준이 사용자가 지정한 값과 같도록 합니다.
Tukey 신뢰 구간 예제
메모리 칩의 반응 시간을 측정하기 위해 5개의 제조업체에서 제작한 25개 칩을 표본으로 추출했습니다.
다섯 공장 간의 10개 비교를 모두 살펴 어떤 평균이 다른지 구체적으로 확인하려고 합니다. Tukey의 방법을 사용하여 전체 비교 집합의 모임 오류율을 0.05로 지정합니다(95% 동시 신뢰 수준과 동일함). Minitab의 계산에 따르면 95% 결합 신뢰 수준을 얻기 위해서는 10개의 개별 신뢰 수준이 99.35%여야 합니다. Tukey 신뢰 구간은 폭이 더 넓고 덜 정확한 모수의 추정치를 제공하지만, 하나 이상의 신뢰 구간에 실제 차이가 포함되지 않을 확률을 최대 5%로 제한합니다. 이러한 맥락에서 모든 신뢰 구간에 유의한 차이가 있음을 의미하는 0이 포함되지 않았는지 확인할 수 있습니다.
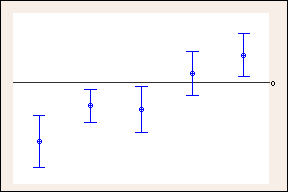
95%의 개별 신뢰 수준을 사용한 신뢰 구간
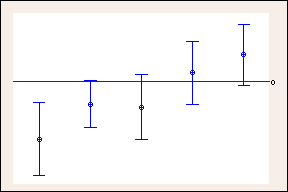
Tukey 방법에서 95% 결합 신뢰 수준을 얻기 위해 99.35%의 개별 신뢰 수준을 사용한 신뢰 구간
95% 신뢰 구간을 이전 예에서 Tukey의 방법에 사용되는 더 폭이 넓은 99.35% 신뢰 구간과 비교합니다. 0 위치의 기준선은 폭이 더 넓은 Tukey 신뢰 구간에 따라 어떻게 결론이 바뀔 수 있는지 보여줍니다. 신뢰 구간이 0을 포함하면 차이가 없음을 나타냅니다. 공간이 충분하지 않기 때문에 10개 비교 중 5개만 표시합니다.
