주효과도를 사용하여 하나 이상의 요인에 대한 수준 평균 간의 차이를 조사할 수 있습니다. 요인 수준에 따라 반응에 다른 영향을 미치면 주효과가 존재합니다. 주효과도에서는 선으로 연결되는 각 요인 수준의 반응 평균을 그래프로 표시합니다.
를 선택하면 Minitab에서 데이터 평균을 사용하는 그림을 생성합니다. 모형을 적합한 후 저장된 모형을 사용하여 적합 평균을 사용하는 그림을 생성할 수 있습니다.
예
예를 들어, 비료 회사 B에서 자사 제품을 사용한 식물에서 측정한 성장률을 회사 A의 비료를 사용한 식물과 비교하려고 합니다. 두 곳에서 두 가지 비료를 검사했습니다. 다음 그림은 이러한 두 요인의 주효과도입니다.
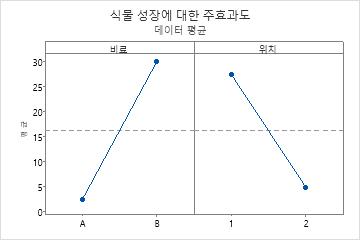
선이 수평이 아니기 때문에 비료가 식물의 성장률에 영향을 미치는 것으로 보입니다. 비료 B의 평균 식물 성장률이 비료 A보다 더 높습니다. 위치도 식물의 성장률에 영향을 미칩니다. 위치 1의 평균 식물 성장률이 위치 2보다 더 높습니다. 기준선은 전체 평균을 나타냅니다.
일반적인 패턴
- 선이 수평(x-축에 평행)이면 주효과가 없습니다. 요인의 각 수준은 반응에 같은 방식으로 영향을 미치고, 반응 평균은 모든 요인 수준에서 동일합니다.
- 선이 수평이 아니면 주효과가 존재합니다. 요인의 수준별로 반응에 미치는 영향이 다릅니다. 선의 기울기가 더 가파를수록 주효과의 크기가 더 큽니다.
주효과도에는 교호작용이 표시되지 않습니다. 요인 간의 교호작용을 확인하려면 교호작용도를 사용하십시오.
중요
패턴이 통계적으로 유의한지 확인하려면 적절한 검정을 수행해야 합니다.
