다변량 분산 분석의 정의
- 검정력 증가
- 반응 변수 간 데이터의 공분산 구조를 사용하여 평균의 동일성을 동시에 검정할 수 있습니다. 이러한 추가 정보는 반응 변수들이 상관되어 있는 경우, 너무 작아서 개별 분산 분석을 통해서는 탐지할 수 없는 차이를 탐지하는 데 도움이 됩니다.
- 다변량 반응 패턴 탐지
- 요인이 단일 반응에 영향을 미치는 대신 반응 간의 관계에 영향을 미칠 수도 있습니다. 분산 분석에서는 다음 그림에 표시된 것처럼 이러한 다변량 패턴을 탐지하지 못합니다.
- 모임 오류율 관리
- 귀무 가설을 잘못 기각할 가능성은 분산 분석을 한 번 더 실행할 때마다 증가합니다. 다변량 분산 분석을 한 번 실행하여 모든 반응 변수를 동시에 검정하면 모임 오류율을 알파 수준과 동일하게 유지할 수 있습니다.
예를 들어, 여러 유형의 합금(1, 2 및 3)이 건축 제품의 강도와 유연성에 미치는 영향을 조사하려고 합니다. 분산 분석을 두 번 수행했지만 결과가 유의하지 않습니다. 따라서 개별 값 그림을 사용하여 두 반응 변수의 원시 데이터를 표시합니다. 이러한 그림에서는 분산 분석의 결과가 유의하지 않음을 시각적으로 확인할 수 있습니다.
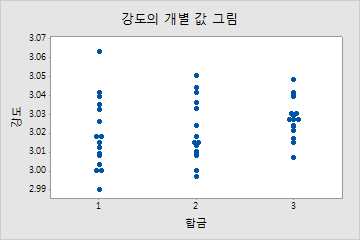
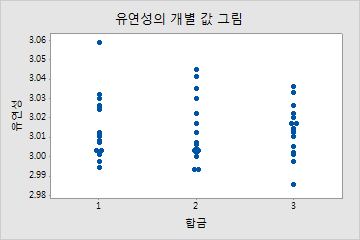
반응 변수들이 상관되어 있기 때문에 다변량 분산 분석을 수행합니다. 이번에는 p-값이 0.05보다 작아서 결과가 유의합니다. 결과를 더 잘 이해하기 위해 산점도를 작성합니다.
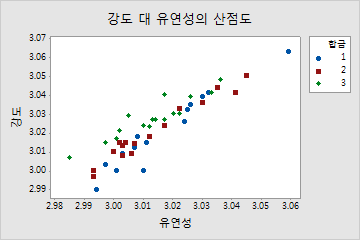
개별 값 그림은 일변량의 관점에서 합금의 유형이 강도나 유연성에 유의하게 영향을 미치지 않는다는 것을 나타냅니다. 그러나 동일한 데이터의 산점도를 보면 합금의 유형에 따라 두 반응 변수 간의 관계가 달라지는 것을 알 수 있습니다. 즉, 유연성이 일정한 상태에서 3번 합금이 일반적으로 1번과 2번 합금에 비해 강도 점수가 더 높습니다.
참고
일반적으로 분석을 실행하기 전에 데이터를 그래프로 표시해야 합니다. 이렇게 하면 어떤 접근 방법이 적절한지 결정하는 데 도움이 됩니다.
다변량 분산 분석에 포함되어 있는 다변량 검정
- Wilk의 검정
- Lawley-Hotelling 검정
- Pillai의 검정
- Roy의 최대근 검정
- 표본간 제곱합이라고도 하는 각 항과 관련된 H(가설) 행렬
- 표본내 제곱합이라고도 하는 검정의 오차와 관련된 E(오차) 행렬
SSCP 행렬은 가설 행렬을 요청할 때 표시됩니다.
검정 통계량을 H, E 또는 H 및 E로 나타내거나 E-1 H의 고유값으로 표시할 수 있으며, 이러한 고유값이 표시되도록 요청할 수 있습니다. 고유값이 반복되면 해당하는 고유 벡터는 고유하지 않으며, 이 경우 Minitab에서 표시하는 고유 벡터는 책이나 다른 소프트웨어의 고유 벡터와 일치하지 않을 수 있습니다. 그러나 다변량 분산 분석 검정은 항상 고유합니다.
