공변량의 정의
공변량은 일반적으로 분석 분석과 실험계획법에 사용됩니다. 이러한 모형에서 공변량은 데이터를 수집하는 동안 제어되지 않는 계량형 변수입니다. 공변량을 포함하면 모형에 실험에서 측정되었지만 랜덤화되거나 제어되지 않은 입력 변수를 포함하고 이에 대해 조정할 수 있습니다. 공변량을 추가하면 모형의 정확도가 크게 개선되며 최종 분석 결과에 유의한 영향을 미칠 수 있습니다. 모형에 공변량을 추가하면 모형의 오차를 줄여 요인 검정의 검정력을 늘릴 수 있습니다. 일반적인 공변량으로는 주변 온도, 습도 및 처리를 적용하기 전의 부품 또는 대상의 특성 등이 있습니다.
예를 들어, 한 엔지니어가 네 가지 철강 빔의 부식 수준을 연구하려고 합니다. 엔지니어는 부식 속도를 빠르게 하기 위해 각 빔을 액체 처리제에 노출하지만, 액체의 온도는 제어할 수 없습니다. 온도는 모형에서 고려해야 하는 공변량입니다.
실험계획법에서 엔지니어는 두 가지 유형의 페인트 건조 시간에 대한 공변량, 대기 온도의 효과에 관심이 있을 수도 있습니다.
일반 선형 모형에 공변량 추가 예제
한 섬유 회사에서 세 대의 기계를 사용하여 단섬유를 제조합니다. 회사에서는 섬유의 파손 강도가 기계별로 다른지 여부를 확인하려고 합니다. 회사에서는 각 기계에서 랜덤하게 추출한 5개 섬유의 강도 및 지름에 대한 데이터를 수집합니다. 섬유 강도는 지름과 관련이 있기 때문에 공변량으로 사용할 경우를 위해 섬유 지름도 기록합니다.
| C1 | C2 | C3 |
|---|---|---|
| 기계 | 지름 | 강도 |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- 공변량과 반응 사이에 선형 관계가 있는지 확인합니다. Minitab에서 적합선 그림으로 데이터를 분석하여 선형 관계가 있는지 확인할 수 있습니다.
- 을 선택합니다.
- 반응(Y)에 강도를 입력합니다.
- 예측 변수(X)에 지름을 입력합니다.
- 데이터가 적합선에 얼마나 가깝고 R2이 "완전 적합"(100%)에 얼마나 가까운지 평가합니다.
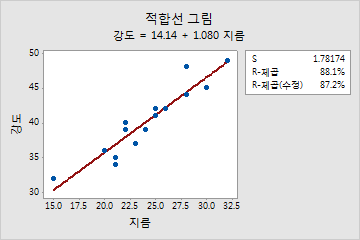
적합선 그림은 지름과 강도 사이에 강한 선형 관계(87.2%)가 있음을 나타냅니다.
- 공변량을 사용하여 GLM 분석을 수행합니다.
- 을 선택합니다.
- 반응에 강도를 입력합니다.
- 요인에 기계를 입력합니다.
- 공변량에 지름을 입력합니다.
- 확인을 클릭합니다.
섬유 생산 데이터에 대해 Minitab에서는 다음 결과를 표시합니다.
일반 선형 모형: 강도 대 지름, 기계
분산 분석 출처 DF Adj SS Adj MS F-값 P-값 지름 1 178.014 178.014 69.97 0.000 기계 2 13.284 6.642 2.61 0.118 오차 11 27.986 2.544 적합성 결여 7 18.486 2.641 1.11 0.487 순수 오차 4 9.500 2.375 총계 14 346.400기계에 대한 F-통계량은 2.61이고 p-값은 0.118입니다. p-값이 0.05보다 크기 때문에 5% 유의 수준에서 기계별로 섬유 강도가 다르다는 귀무 가설을 기각할 수 없습니다. 모든 기계의 섬유 강도가 동일하다고 가정할 수 있습니다. 지름(공변량)의 F-통계량은 69.97이고 p-값은 0.000입니다. 이는 공변량 효과가 유의하다는 것을 나타냅니다. 즉, 지름이 섬유 강도에 유의한 영향을 미칩니다.
이제 공변량을 제외하고 분석을 다시 실행한다고 가정합니다. 이 경우 다음과 같은 결과가 표시됩니다.
일반 선형 모형: 강도 대 기계
분산 분석 출처 DF Adj SS Adj MS F-값 P-값 기계 2 140.4 70.20 4.09 0.044 오차 12 206.0 17.17 총계 14 346.4F-통계량은 4.09이고 p-값은 0.044입니다. 모형에 공변량이 없는 경우 5% 유의 수준에서 귀무 가설을 기각하고 기계별로 섬유 강도가 다르다는 결론을 내릴 수 있습니다.
이 결론은 공변량을 사용하여 분석을 수행할 때와 완전히 반대입니다. 이 예는 공변량을 포함하지 않을 경우 잘못된 분석 결과가 나올 수 있다는 것을 보여줍니다.
