일원 분산 분석의 다중 비교에 대한 방법 및 공식

Minitab에서는 Tukey의 방법, Fisher의 방법, Dunnett의 방법, Hsu의 MCB, Games-Howell 등 일원 분산 분석에서 여러 개의 요인 평균을 비교하기 위한 5가지 방법을 제공합니다. 이러한 검정의 공식은 아래 나열되어 있습니다.

표기법

용어	설명
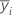	i번째 요인 수준에 대한 표본 평균
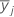	j번째 요인 수준에 대한 표본 평균
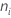	수준 i의 관측치 수
r	수준 수
s	합동 표준 편차 또는 MSE의 제곱근
u	오차에 대한 자유도
α	제1종 오류를 범할 동시 확률
α*	제1종 오류를 범할 개별 확률

Tukey:

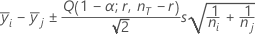
여기서 Q = 자유도가 r 및 n_T - r인 스튜던트화 범위 분포의 상위 α 백분위수입니다.

동시 오류율에서 개별 오류율을 찾으려면 다음 공식을 사용하십시오.

Fisher:

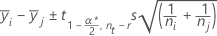
여기서 t = 자유도가 u인 스튜던트 t 분포의 상위 α/2 점입니다.

개별 오류율에서 동시 신뢰 수준을 찾으려면 다음 공식을 사용하십시오.

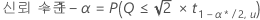
Dunnett:

d를 계산하는 방법은 Hsu¹의 63페이지를 참조하십시오.

Hsu의 MCB:

여기서는 모든 그룹 크기가 n인 경우에 대한 공식을 제공합니다. 그룹 크기가 같지 않은 경우의 공식은 Hsu¹를 참조하십시오. 가장 큰 평균을 가장 적합한 값으로 선택하고 i번째 평균 - 나머지 중 가장 큰 평균을 계산한다고 가정합니다.

하한점은 0과 다음 값 중 작은 값입니다.

상한점은 0과 다음 값 중 큰 값입니다.

d를 계산하는 방법은 Hsu¹의 83페이지를 참조하십시오.

가장 작은 수준 평균이 가장 적합한 값인 경우 max를 min으로 바꾸는 것을 제외하고 공식이 같습니다.

Games-Howell 및 Welch 검정

Welch 검정 통계량은 다음과 같이 계산됩니다.

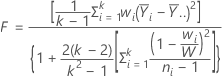
Welch 검정에 대한 p-값은 분모 자유도가 k - 1(여기서 k는 X 수준의 수)이고 분모 자유도가 다음과 같이 계산되는 F 분포의 위쪽 꼬리 확률입니다.

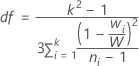
μ_i - μ_j에 대한 비교 구간은 다음과 같습니다.

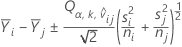
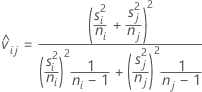
수정된 P-값을 계산하기 위해 사용되는 T-비율은 다음과 같습니다.

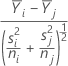
설명:

범주형 요인의 i번째 수준에서 j번째 반응은 다음과 같습니다.

Y_ij, j = 1, ... , n_i; i = 1, ... k

i번째 수준에서 평균 반응은 다음과 같습니다.

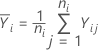
표본 분산은 다음과 같습니다.

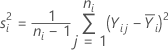
수준 i에 대한 가중치는 다음과 같습니다.

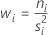
모든 가중치의 합은 다음과 같습니다.

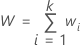
반응의 전체 가중 평균은 다음과 같습니다.

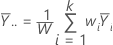
감사의 글

다중 비교를 설계하고 구현할 수 있도록 도와주신 데 대해 Jason C. Hsu에게 깊은 감사를 드립니다.

[1] J.C. Hsu (1996). Multiple Comparisons, Theory and methods. Chapman & Hall.