원하는 방법 또는 공식을 선택하십시오.
표기법
표기법은 분산 분석 모형을 이해하는 데 있어 중요합니다. 일원 분산 분석에 사용되는 표기법이 아래에 나열되어 있습니다.
| 용어 | 설명 |
|---|---|
| r | 요인의 수준 수, i = 1 ...r |
| i | 지정된 요인 수준 |
| j | 특정 요인 수준에 대해 지정된 사례, j = 1 ...ni |
| yij | i번째 요인 수준에 대한 반응의 j번째 관측치 |
| ni | i번째 요인 수준에 대한 관측치 수 |
| nT | 전체 사례 수 |
| μi | i번째 요인 수준에서 관측치의 실제 평균 |
| yi. | i번째 요인 수준에서 관측치의 합계 |
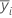 | i번째 요인에 대한 반응의 평균 |
모형 적합
공식
일원 분산 분석 모형은 여러 가지 방법으로 지정할 수 있습니다. 셀 평균 모형은 다음과 같습니다.
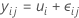
요인 수준의 모든 관측치는 동일한 기대값 μi을 갖습니다. μi는 상수이기 때문에 모든 관측치는 요인 수준에 관계없이 동일한 분산을 갖습니다.
분산 분석에서는 최소 제곱 추정 방법이 모형을 적합하고 모수 μi에 대한 추정치를 제공하기 위해 사용됩니다.
일원 분산 분석에 대한 가설 검정은 다음과 같습니다.
H0: μ1 = μ2= … = μr
H1: At least one mean is not equal to the others
표기법
| 용어 | 설명 |
|---|---|
| μi | i번째 요인 수준에서 모수 또는 관측치의 실제 평균 |
| εij | 독립적이며 평균이 0이고 분산이 σ2로 일정한 정규 분포를 따르는 오차 |
