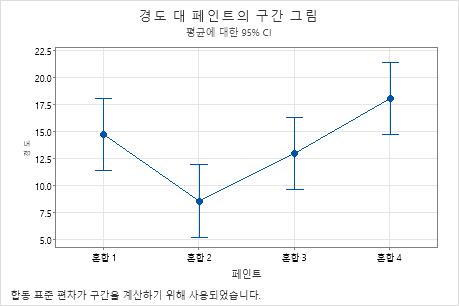
한 화학 엔지니어가 네 가지 혼합 페인트의 경도를 비교하려고 합니다. 각 혼합 페인트의 표본 6개를 금속 조각에 칠하고 금속 조각을 건조시켰습니다. 그런 다음 각 표본의 경도를 측정했습니다. 평균의 동일성을 검정하고 평균 쌍 간의 차이를 평가하기 위해 분석가는 다중 비교와 함께 일원 분산 분석을 사용합니다.
- 표본 데이터페인트경도.MWX을 엽니다.
- 을 선택합니다.
- 반응 데이터가 모든 요인 수준에 대해 별도의 열에 있음을 선택합니다.
- 반응 변수에 경도을 입력합니다.
- 요인에 페인트을 입력합니다.
- 비교 버튼을 클릭한 다음 Tukey을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
페인트 경도 분산 분석의 p-값은 0.05보다 작습니다. 이 결과는 혼합 페인트의 경도가 유의하게 서로 다르다는 것을 나타냅니다. 엔지니어는 일부 그룹 평균이 다르다는 것을 알고 있습니다.
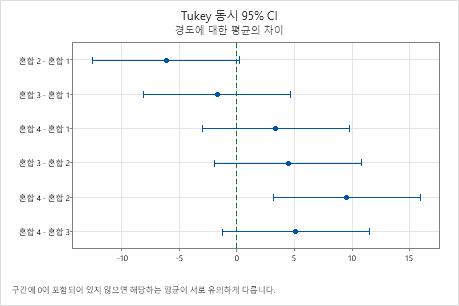
엔지니어는 Tukey 비교 결과를 사용하여 그룹 쌍 간의 차이가 통계적으로 유의한지 여부를 공식적으로 검정합니다. Tukey 동시 신뢰 구간이 포함된 그래프는 혼합 2와 4의 평균 간의 차이에 대한 신뢰 구간이 3.114에서 15.886까지라는 것을 보여줍니다. 이 범위에는 0이 포함되지 않으므로 이 평균들 간의 차이가 유의합니다. 엔지니어는 이 차이 추정치를 사용하여 차이가 실제적으로 유의한지 여부를 확인할 수 있습니다.
나머지 평균 쌍에 대한 신뢰 구간에는 모두 0이 포함되므로 차이가 유의하지 않습니다.
낮은 예측 R2(24.32%) 값은 모형이 새 관측치에 대한 부정확한 예측을 생성한다는 것을 나타냅니다. 이는 그룹의 표본 크기가 작기 때문일 수 있습니다. 따라서 엔지니어는 모형을 사용하여 표본 데이터를 넘어 일반화하지 말아야 합니다.
방법
| 귀무 가설 | 모든 평균이 동일합니다. |
|---|
| 대립 가설 | 평균이 모두 같지 않음 |
|---|
| 유의 수준 | α = 0.05 |
|---|
요인 정보
| 페인트 | 4 | 혼합 1, 혼합 2, 혼합 3, 혼합 4 |
|---|
분산 분석
| 페인트 | 3 | 281.7 | 93.90 | 6.02 | 0.004 |
|---|
| 오차 | 20 | 312.1 | 15.60 | | |
|---|
| 총계 | 23 | 593.8 | | | |
|---|
모형 요약
| 3.95012 | 47.44% | 39.56% | 24.32% |
평균
| 혼합 1 | 6 | 14.73 | 3.36 | (11.37, 18.10) |
|---|
| 혼합 2 | 6 | 8.57 | 5.50 | (5.20, 11.93) |
|---|
| 혼합 3 | 6 | 12.98 | 3.73 | (9.62, 16.35) |
|---|
| 혼합 4 | 6 | 18.07 | 2.64 | (14.70, 21.43) |
|---|
Tukey의 방법 및 95% 신뢰 구간을 사용한 그룹화 정보
| 혼합 4 | 6 | 18.07 | A | |
|---|
| 혼합 1 | 6 | 14.73 | A | B |
|---|
| 혼합 3 | 6 | 12.98 | A | B |
|---|
| 혼합 2 | 6 | 8.57 | | B |
|---|