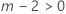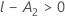고정 효과 항의 검정
고정 효과 항의 검정은 F 검정입니다. 검정의 귀무 가설은 검정이 고정 요인 항에 대한 것인지 공변량 항에 대한 것인 지에 따라 다릅니다. 고정 요인 항의 경우 귀무 가설은 항이 반응에 유의하게 영향을 미치지 않는다는 것입니다. 공변량 항의 경우 귀무 가설은 반응과 공변량 항 간에 연관성이 존재하지 않는다는 것입니다.
Minitab에서는 고정 효과 항을 검정하기 위해 Kenward-Roger 근사와 Satterthwaite 근사, 두 가지 방법을 제공합니다. Kenward-Roger 근사에 대한 자세한 내용은 Kenward and Roger를 참고하십시오.1. Satterthwaite 근사에 대한 자세한 내용은 Giesbrecht and Burns를 참고하십시오. 2, Fai and Cornelius. 3
F-통계량의 분모 자유도 및 F-통계량은 서로 다르게 계산됩니다. 주어진 F-통계량에 대한 분자 자유도와 p-값은 두 방법 모두 동일하게 계산됩니다.
Kenward-Roger 근사
Kenward-Roger 근사는 고정 효과 항의 통계적 유의성을 검정하는 한 가지 방법입니다.
F-통계량
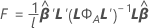
설명:
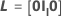
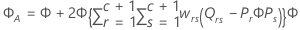
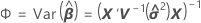
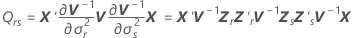
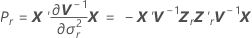
표기법
| 용어 | 설명 |
|---|---|
| l | 분자 자유도(검정할 항의 모수 수) |
| 0 | 성분이 0개인 행렬 |
| Il | 크기가 l인 단위 행렬 |
| c + 1 | 분산 성분의 수 |
| wrs | (점근 분산-공분산 행렬의 r, s)번째 성분:  |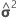
| V−1 | 분산-공분산 행렬의 역행렬 |
표기법에 대한 자세한 내용은 방법 섹션에서 확인하십시오.
분모 자유도
설명:
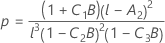
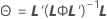
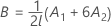
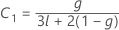
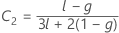
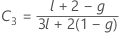
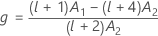
Kenward 및 Roger λ
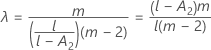
두 조건 중 하나가 참이 아니면 λ = 1입니다.
귀무 가설 하에서 람다 × F는 자유도가 DF Num, DF Den인 F 분포를 점근적으로 따릅니다. P-값의 계산에서는 이 속성을 사용합니다.
Satterthwaite 근사
Satterthwaite 근사는 고정 효과 항의 통계적 유의성을 검정하는 한 가지 방법입니다.
F-통계량
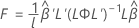
여기서 L 및 
의 정의는 Kenward-Roger 근사와 같습니다.
분모 자유도
자유도를 결정하는 절차에는 여러 단계가 있습니다.
-
고정 효과 모수 벡터 추정치의 분산에 대한 분광 분해를 수행합니다.
여기서 P는 고유 벡터의 직교 행렬이고 D는 고유 벡터의 대각 행렬이며, 둘 다 크기가 l × l입니다.
-
lr을 P'L의 r 번째 행(r = 1, ..., l)으로 정의하고
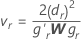설정합니다. 여기서 dr은 D의 r번째 대각 원소 W는
의 점근 분산 공분산 행렬이며 gr은 다음과 같은 요소의 경사 벡터입니다.
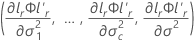
설명:
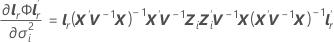
i = 1, …, c 그리고
-
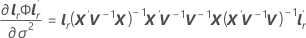
다음과 같이 설정합니다.
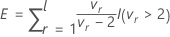
설명
는 
인 항을 제거하는 지시 함수입니다. -
분모의 자유도는 E의 값에 따라 달라집니다.
- E > l인 경우 자유도는 다음과 같습니다.
- 그렇지 않은 경우 DF Den = 1입니다.
- E > l인 경우 자유도는 다음과 같습니다.
분자 자유도(DF Num)
| 효과 | DF |
|---|---|
| 고정 요인 |  |
| 공변량 | 1 |
| 고정 요인이 포함된 교호작용 |  |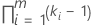
표기법
| 용어 | 설명 |
|---|---|
| k | 고정 요인 항의 수준 수 |
| m | 교호작용의 요인 수 |
p-값 - 고정 효과의 검정
표기법
| 용어 | 설명 |
|---|---|
 | 자유도가 각각 DF Num 및 DF Den인 F-분포의 누적분포함수 |
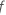 | 항에 대해 계산된 F-값 |
