한 연구자가 임의로 선택된 네 개의 밭에서 6개의 자주개자리 품종의 수확량을 검사합니다. 각 밭에서 각 품종의 수확량을 기록했습니다.
연구자는 자주개자리의 품종이 평균 수확량에 영향을 미치는지 여부를 알려고 합니다. 연구자는 4개의 밭에서 데이터를 수집할 수 있습니다. 그러나 연구자는 실험에 포함되지 않은 밭에서 자주개자리가 어떻게 자라는지 모형화하려고 합니다. 따라서 연구자는 자주개자리가 자라는 밭을 변량 요인으로 설정합니다. 연구자는 혼합 효과 모형을 사용하여 고정 및 랜덤 효과를 함께 평가합니다.
- 표본 데이터 자주개자리.MWX을 엽니다.
- 을 선택합니다.
- 반응에 수확량을 입력합니다.
- 변량 요인(필수)에 밭을 입력합니다.
- 고정 요인에 품종을 입력합니다.
- 그래프을 클릭합니다.
- 사용할 잔차에서 조건부 표준화 잔차을 선택합니다.
- 잔차 그림에서 네 개 모두을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
분산 성분 표에서 밭에 대한 p-값은 0.124입니다. 가설 검정은 분산 성분이 0과 다르다는 증거를 보여주지 않습니다.오차의 분산 성분에 대한 p-값은 0.003입니다. p-값이 유의 수준 0.05보다 작기 때문에 연구자는 오차에 대한 분산 성분이 0이 아니라는 결론을 내릴 수 있습니다.
고정 요인 항인 품종에 대한 p-값은 약 0으로, 하나 이상의 자주개자리 유형의 수확량에 대한 효과가 다른 다섯 가지 유형과 유의하게 다르다는 것을 보여줍니다.
주효과에 대한 계수가 각 수준 평균과 전체 평균 간의 차이를 나타냅니다. 예를 들어, 품종 1은 전체 평균보다 약 0.385 단위가 큰 자주개나리 밭과 연관성이 있습니다. 이 계수에 대한 p-값은 약 0으로, 품종 1의 수확량에 대한 효과가 품종 항의 다른 수준 효과와 유의하게 다르다는 것을 나타냅니다. 통계적으로 같은 수준 효과와 통계적으로 서로 다른 수준 효과를 확인하기 위해 연구자는 항에 대한 다중 비교 분석을 수행하기로 계획합니다.
R2 값은 모형이 수확량 변동의 약 92%를 설명한다는 것을 보여줍니다. R-제곱(수정)도 약 90.2%로 높습니다. 연구자는 예측 변수의 수가 서로 다른 모형을 비교하기 위해 이 값을 사용합니다.
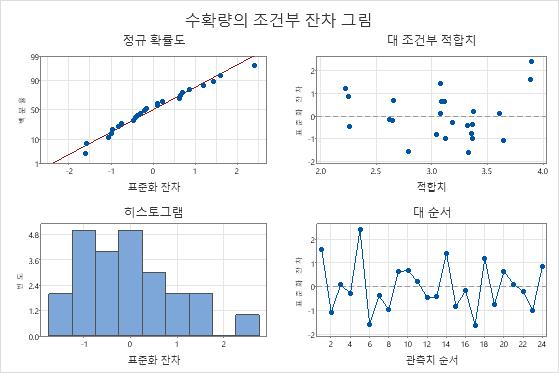
관측치 1과 5는 표준화 잔차가 2보다 크기 때문에 비정상적 관측치입니다. 연구자는 이 관측치에 대한 반응 값이 올바른지 확인하기 위해 데이터를 조사합니다.
정규 확률도의 잔차는 직선에 근사하며, 점들은 잔차 대 적합치 그림에서 0을 중심으로 랜덤하게 퍼져 있는 것으로 보입니다.
방법
| 분산 추정 | 제한적 최대우도법 |
|---|---|
| 고정 효과의 DF | Kenward-Roger |
요인 정보
| 요인 | 유형 | 수준 | 값 |
|---|---|---|---|
| 밭 | 랜덤 | 4 | 1, 2, 3, 4 |
| 품종 | 고정 | 6 | 1, 2, 3, 4, 5, 6 |
분산 성분
| 출처 | 분산 | 총계의 % | SE 분산 | Z-값 | P-값 |
|---|---|---|---|---|---|
| 밭 | 0.077919 | 72.93% | 0.067580 | 1.152996 | 0.124 |
| 오차 | 0.028924 | 27.07% | 0.010562 | 2.738613 | 0.003 |
| 총계 | 0.106843 |
고정 효과의 검정
| 항 | DF 분자 | DF 분모 | F-값 | P-값 |
|---|---|---|---|---|
| 품종 | 5.00 | 15.00 | 26.29 | 0.000 |
모형 요약
| S | R-제곱 | R-제곱(수정) | AICc | BIC |
|---|---|---|---|---|
| 0.170071 | 92.33% | 90.20% | 12.54 | 13.52 |
계수
| 항 | 계수 | SE 계수 | DF | T-값 | P-값 |
|---|---|---|---|---|---|
| 상수 | 3.094583 | 0.143822 | 3.00 | 21.516692 | 0.000 |
| 품종 | |||||
| 1 | 0.385417 | 0.077626 | 15.00 | 4.965016 | 0.000 |
| 2 | 0.145417 | 0.077626 | 15.00 | 1.873287 | 0.081 |
| 3 | 0.107917 | 0.077626 | 15.00 | 1.390205 | 0.185 |
| 4 | -0.319583 | 0.077626 | 15.00 | -4.116938 | 0.001 |
| 5 | 0.395417 | 0.077626 | 15.00 | 5.093838 | 0.000 |
비정상적 관측치에 대한 주변 적합치 및 진단
| 관측 | 수확량 | 적합치 | 잔차 | 표준화 잔차 | |
|---|---|---|---|---|---|
| 1 | 4.100000 | 3.480000 | 0.620000 | 2.190221 | R |
| 5 | 4.220000 | 3.490000 | 0.730000 | 2.578808 | R |
비정상적 관측치에 대한 조건부 적합치 및 진단
| 관측 | 수확량 | 적합치 | 잔차 | 표준화 잔차 | |
|---|---|---|---|---|---|
| 5 | 4.220000 | 3.895339 | 0.324661 | 2.400733 | R |