이 항목의 내용
1단계: 모든 반응에서 평균의 동일성 검정
- p-값 ≤ α: 평균 간의 차이가 통계적으로 유의합니다.
- p-값이 유의 수준보다 작거나 같으면 평균 간의 차이가 통계적으로 유의하다는 결론을 내릴 수 있습니다.
- p-값 > α: 평균 간의 차이가 통계적으로 유의하지 않습니다.
- p-값이 유의 수준보다 크면 평균 간의 차이가 통계적으로 유의하다는 결론을 내릴 수 없습니다. 항 없이 모형을 다시 적합시킬 수도 있습니다.
- 주효과가 유의하면 모형의 모든 반응에 걸쳐 요인에 대한 수준 평균들이 서로 유의하게 다릅니다.
- 교호작용 항이 유의하면 모형이 모든 반응에 걸쳐 각 요인의 효과가 다른 요인의 수준별로 다릅니다. 이런 이유로 유의한 고차 교호작용에 포함된 항의 개별 효과를 분석하는 것은 의미가 없습니다.
방법에 대한 다변량 분산 분석 검정
| DF | |||||
|---|---|---|---|---|---|
| 기준 | 검정 통계량 | F | 수 | 분모 | P |
| Wilks' | 0.63099 | 16.082 | 2 | 55 | 0.000 |
| Lawley-Hotelling 검정 | 0.58482 | 16.082 | 2 | 55 | 0.000 |
| Pillai's | 0.36901 | 16.082 | 2 | 55 | 0.000 |
| Roy's | 0.58482 | ||||
공장에 대한 다변량 분산 분석 검정
| DF | |||||
|---|---|---|---|---|---|
| 기준 | 검정 통계량 | F | 수 | 분모 | P |
| Wilks' | 0.89178 | 1.621 | 4 | 110 | 0.174 |
| Lawley-Hotelling 검정 | 0.11972 | 1.616 | 4 | 108 | 0.175 |
| Pillai's | 0.10967 | 1.625 | 4 | 112 | 0.173 |
| Roy's | 0.10400 | ||||
방법*공장에 대한 다변량 분산 분석 검정
| DF | |||||
|---|---|---|---|---|---|
| 기준 | 검정 통계량 | F | 수 | 분모 | P |
| Wilks' | 0.85826 | 2.184 | 4 | 110 | 0.075 |
| Lawley-Hotelling 검정 | 0.16439 | 2.219 | 4 | 108 | 0.072 |
| Pillai's | 0.14239 | 2.146 | 4 | 112 | 0.080 |
| Roy's | 0.15966 | ||||
주요 결과: P
생산 방법에 대한 p-값은 0.10 유의 수준에서 통계적으로 유의합니다. 제조 공장에 대한 p-값은 모든 검정에 대해 0.10 유의 수준에서 통계적으로 유의하지 않습니다. 공장과 방법의 교호작용에 대한 p-값은 0.10 유의 수준에서 통계적으로 유의합니다. 교호작용이 통계적으로 유의하기 때문에 방법의 효과는 공장에 따라 다릅니다.
2단계: 각 요인에 대해 어느 반응 평균의 차이가 가장 큰지 확인
여러 모형 항의 수준들 사이에서 반응 평균이 어떻게 다른지 평가하려면 고유 분석을 사용합니다. 큰 고유값에 해당하는 고유 벡터에 초점을 맞춰야 합니다. 고유 분석을 표시하려면 에서 고유 분석(결과 표시)을 선택하십시오.
방법에 대한 고유 분석
| 고유값 | 0.5848 | 0.00000 |
|---|---|---|
| 비율 | 1.0000 | 0.00000 |
| 누적 | 1.0000 | 1.00000 |
| 고유 벡터 | 1 | 2 |
|---|---|---|
| 유용성 등급 | 0.144062 | -0.07870 |
| 품질 등급 | -0.003968 | 0.13976 |
주요 결과: 고유값, 고유 벡터
이 결과에서는 방법에 대한 첫 번째 고유값(0.5848)이 두 번째 고유값(0.00000)보다 큽니다. 따라서 첫 번째 고유 벡터에 더 큰 중요성을 부여해야 합니다. 방법의 첫 번째 고유 벡터는 0.144062, -0.003968입니다. 이 벡터 내 가장 큰 절대값은 유용성 등급에 대한 것입니다. 즉, 유용성에 대한 평균이 방법에 대한 요인 수준 간에 가장 차이가 크다는 것을 나타냅니다. 이 정보는 평균 표를 평가하는 데 유용합니다.
3단계: 그룹 평균 간의 차이 평가
평균 표를 사용하면 데이터의 요인 수준 간의 통계적으로 유의한 차이를 파악할 수 있습니다. 각 그룹의 평균은 각 모평균의 추정치를 제공합니다. 통계적으로 유의한 항에 대한 그룹 평균 간의 차이를 찾아보십시오.
주효과의 경우 표에는 각 요인 내 그룹 및 그룹의 평균이 표시됩니다. 교호작용 효과의 경우 표에는 그룹의 모든 가능한 조합이 표시됩니다. 교호작용 항이 통계적으로 유의하면 교호작용 효과를 고려하지 않고 주효과를 해석하지 마십시오.
평균을 표시하려면 에서 일변량 분산 분석을 선택하고 항에 해당하는 최소 제곱 평균 표시에 항을 입력하십시오.
반응에 대한 최소 제곱 평균
| 유용성 등급 | 품질 등급 | |||
|---|---|---|---|---|
| 평균 | 평균의 표준 오차 | 평균 | 평균의 표준 오차 | |
| 방법 | ||||
| 방법 1 | 4.819 | 0.165 | 5.242 | 0.193 |
| 방법 2 | 6.212 | 0.179 | 6.026 | 0.211 |
| 공장 | ||||
| 공장 A | 5.708 | 0.192 | 5.833 | 0.226 |
| 공장 B | 5.493 | 0.232 | 5.914 | 0.273 |
| 공장 C | 5.345 | 0.206 | 5.155 | 0.242 |
| 방법*공장 | ||||
| 방법 1 공장 A | 4.667 | 0.272 | 5.417 | 0.319 |
| 방법 1 공장 B | 4.700 | 0.298 | 5.400 | 0.350 |
| 방법 1 공장 C | 5.091 | 0.284 | 4.909 | 0.334 |
| 방법 2 공장 A | 6.750 | 0.272 | 6.250 | 0.319 |
| 방법 2 공장 B | 6.286 | 0.356 | 6.429 | 0.418 |
| 방법 2 공장 C | 5.600 | 0.298 | 5.400 | 0.350 |
주요 결과: 평균
이 결과에서 평균 표는 평균 유용성 및 품질 등급이 방법, 공장 및 방법*공장 교호작용에 따라 어떻게 달라지는지 보여줍니다. 방법 및 교호작용 항은 0.10 수준에서 통계적으로 유의합니다. 표는 방법 1과 방법 2가 각각 평균 유용성 등급 4.819 및 6.212와 연관되어 있다는 것을 보여줍니다. 이러한 평균 간의 차이는 품질 등급에 해당하는 평균 간의 차이보다 큽니다. 이는 고유 분석 해석을 확인합니다.
그러나 방법*공장 교호작용 항도 통계적으로 유의하므로 교호작용 효과를 고려하지 않고 주효과를 해석하지 마십시오. 예를 들어, 교호작용 항에 대한 표는 방법 1의 경우, 공장 C가 가장 높은 유용성 등급 및 가장 낮은 품질 등급과 연관된다는 것을 보여줍니다. 그러나 방법 2의 경우, 공장 A가 가장 높은 유용성 등급 및 가장 높은 품질 등급과 거의 같은 품질 등급과 연관되어 있습니다.
4단계: 일변량 결과를 평가하여 개별 반응 조사
일반 다변량 분산 분석을 수행할 때 일변량 통계량을 계산하여 개별 반응을 조사할 수 있습니다. 일변량 결과를 통해 데이터의 관계를 더 직관적으로 이해할 수 있습니다. 그러나 일변량 결과는 다변량 결과와 다를 수 있습니다.
일변량 결과를 표시하려면 에서 일변량 분산 분석(결과 표시)을 선택하십시오.
- p-값 ≤ α: 연관성이 통계적으로 유의합니다.
- p-값이 유의 수준보다 작거나 같으면 반응 변수와 항 간에 통계적으로 유의한 연관성이 있다는 결론을 내릴 수 있습니다.
- p-값 > α: 연관성이 통계적으로 유의하지 않습니다.
- p-값이 유의 수준보다 크면 반응 변수와 항 간에 통계적으로 유의한 연관성이 있다는 결론을 내릴 수 없습니다. 항 없이 모형을 다시 적합시킬 수도 있습니다.
- 범주형 요인이 유의하면 일부 수준 평균이 같지 않다는 결론을 내릴 수 있습니다.
- 교호작용 항이 유의하면 요인과 반응의 관계가 항의 다른 요인에 따라 다릅니다. 이 경우에는 교호작용 효과를 고려하지 않고 주효과를 해석해서는 안 됩니다.
- 공변량이 통계적으로 유의하면 공변량 값의 변화가 평균 반응 값의 변화와 연관성이 있다는 결론을 내릴 수 있습니다.
- 다항식 항이 유의하면 데이터에 곡면성이 포함되어 있다는 결론을 내릴 수 있습니다.
유용성 등급에 대한 분산 분석(검정을 위해 수정된 제곱합 사용)
| 출처 | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| 방법 | 1 | 31.264 | 29.074 | 29.0738 | 32.72 | 0.000 |
| 공장 | 2 | 1.366 | 1.499 | 0.7495 | 0.84 | 0.436 |
| 방법*공장 | 2 | 7.099 | 7.099 | 3.5494 | 3.99 | 0.024 |
| 오차 | 56 | 49.754 | 49.754 | 0.8885 | ||
| 총계 | 61 | 89.484 |
품질 등급에 대한 분산 분석(검정을 위해 수정된 제곱합 사용)
| 출처 | DF | Seq SS | Adj SS | Adj MS | F | P |
|---|---|---|---|---|---|---|
| 방법 | 1 | 8.8587 | 9.2196 | 9.2196 | 7.53 | 0.008 |
| 공장 | 2 | 6.7632 | 7.0572 | 3.5286 | 2.88 | 0.064 |
| 방법*공장 | 2 | 0.7074 | 0.7074 | 0.3537 | 0.29 | 0.750 |
| 오차 | 56 | 68.5900 | 68.5900 | 1.2248 | ||
| 총계 | 61 | 84.9194 |
주요 결과: p-값
이 결과에서 방법의 주효과 및 방법*공장 교호작용에 대한 p-값은 유용성 등급에 대한 모형의 0.10 수준에서 통계적으로 유의합니다. 방법과 모형에 대한 주효과 모두 품질 등급에 대한 모형에서 통계적으로 유의합니다. 이러한 변수의 변경이 반응 변수의 변경과 연관되어 있다는 결론을 내릴 수 있습니다.
5단계: 모형이 분석의 가정을 충족하는지 여부 확인
모형이 적절하고 분석의 가정을 충족하는지 여부를 확인하려면 잔차 그림을 사용합니다. 가정이 충족되지 않으면 모형이 데이터에 적합하지 않은 것이므로 결과를 해석할 때 주의해야 합니다.
일반 다변량 분산 분석을 수행하는 경우 Minitab에서는 모형의 모든 반응 변수에 대해 잔차 그림을 표시합니다. 모든 반응 변수에 대한 잔차 그림에서 모형이 가정을 충족한다는 것을 나타내는지 여부를 확인해야 합니다.
잔차 그림의 패턴을 처리하는 방법에 대한 자세한 내용을 보려면 일반 다변량 분산 분석의 잔차 그림으로 이동하여 페이지 상단의 리스트에서 잔차 그림의 이름을 클릭하십시오.
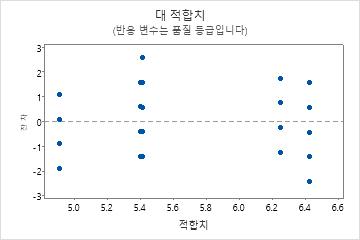
잔차 대 적합치 그림
잔차가 랜덤하게 분포되어 있고 잔차의 분산이 일정하다는 가정을 확인하려면 잔차 대 적합치 그림을 사용하십시오. 이상적으로는 점들이 식별 가능한 패턴 없이 0의 양쪽에 랜덤하게 분포해야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 적합치에 대해 잔차가 부채꼴 모양으로 흩어져 있거나 고르지 않게 퍼져 있음 | 일정하지 않은 분산 |
| 곡선 | 고차 항 누락 |
| 한 점이 0에서 멀리 떨어져 있음 | 특이치 |
| 다른 점에서 x 방향으로 멀리 떨어져 있는 점 | 영향력 있는 점 |
잔차 대 순서 그림
추세
이동
주기
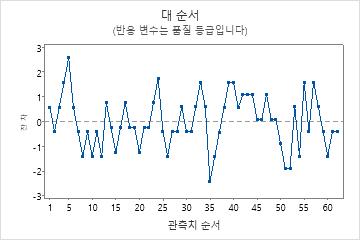
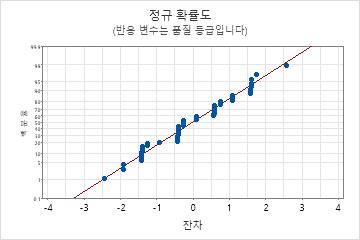
잔차 정규 확률도
잔차가 정규 분포를 따른다는 가정을 확인하려면 잔차의 정규 확률도를 사용하십시오. 잔차의 정규 확률도는 대략 직선을 따라야 합니다.
| 패턴 | 패턴이 나타내는 내용 |
|---|---|
| 직선이 아님 | 비정규성 |
| 선에서 멀리 떨어져 있는 점 | 특이치 |
| 기울기 변화 | 식별되지 않은 변수 |