S
S는 데이터 값과 적합치 간 거리의 표준 편차를 나타냅니다. S는 반응값의 단위로 측정됩니다.
해석
S는 모형이 반응을 얼마나 잘 설명하는지 평가하기 위해 사용합니다. S는 반응 변수 단위로 측정되며, 데이터 값이 적합치로부터 얼마나 떨어져 있는지 나타냅니다. S의 값이 낮을수록 모형이 반응을 더 잘 설명합니다. 그러나 낮은 S 값 자체는 모형이 모형 가정을 충족한다는 것을 나타내지 않습니다. 가정을 확인하려면 잔차 그림을 확인해야 합니다.
예를 들어, 한 감자 칩 회사에서 용기당 부스러진 감자 칩의 백분율에 영향을 미치는 요인을 살펴보려고 합니다. 모형을 유의한 예측 변수로 요약하고 S가 1.79로 계산됩니다. 이 결과는 적합치 주변 데이터 점의 표준 편차가 1.79라는 것을 나타냅니다. 모형을 비교하는 경우 1.79보다 작은 값은 더 좋은 적합치를 나타내고 더 큰 값은 더 나쁜 적합치를 나타냅니다.
R-제곱
R2은 모형에 의해 설명되는 반응 내 변동의 백분율입니다. 이 값은 1 빼기 오차 제곱합(모형에 의해 설명되지 않는 변동) 대 총 제곱합(모형 내 총 변동)의 비율입니다.
해석
모형이 데이터를 얼마나 잘 적합시키는지 확인하려면 R2을 사용합니다. R2 값이 클수록 모형이 데이터를 더 잘 적합시킵니다. R2은 항상 0%에서 100% 사이입니다.
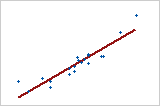
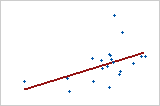
-
모형에 예측 변수를 추가하면 R2은 항상 증가합니다. 예를 들어, 최량 예측 변수가 5개인 모형은 최량 예측 변수가 4개인 모형보다 항상 R2 값이 큽니다. 따라서 R2은 같은 크기의 모형을 비교할 때 가장 유용합니다.
-
작은 표본은 반응과 예측 변수 간 관계의 강도에 대한 정확한 추정치를 제공하지 않습니다. 예를 들어, 더 정확한 R2이 필요하면 더 큰 표본을 사용해야 합니다(일반적으로 40 이상).
-
적합도 통계량은 모형이 데이터를 얼마나 잘 적합시키는 지에 대한 하나의 측도에 지나지 않습니다. 모형에 바람직한 값이 있더라도 해당 모형이 모형 가정을 충족하는지 확인하려면 잔차 그림을 확인해야 합니다.
R-제곱(수정)
수정 R2은 관측치 수에 상대적인 모형에 있는 예측 변수의 수에 따라 수정되고 모형에 의해 설명되는 반응 내 변동의 백분율입니다. 수정 R2은 1에서 전체 평균 제곱(MS 전체)에 대한 평균 오차 제곱(MSE)을 뺀 값의 비율로 계산됩니다.
해석
예측 변수 수가 다른 여러 모형을 비교하려면 수정 R2을 사용합니다. 모형에 예측 변수를 추가하면 모형이 실제로 개선되지 않더라도 R2은 항상 증가합니다. 수정 R2 값은 모형의 예측 변수 수에 통합되어 올바른 모형을 선택하는 데 도움이 됩니다.
| 모형 | 감자 % | 냉각 비율 | 조리 온도 | R2 | 수정 R2 |
|---|---|---|---|---|---|
| 1 | X | 52% | 51% | ||
| 2 | X | X | 63% | 62% | |
| 3 | X | X | X | 65% | 62% |
첫 번째 모형은 50%보다 큰 R2을 생성합니다. 두 번째 모형은 모형에 냉각 비율을 추가합니다. 수정 R2이 중가하며, 이는 냉각 비율이 모형을 개선한다는 것을 나타냅니다. 세 번째 모형은 조리 온도를 추가하며, R2은 증가하지만 수정 R2은 증가하지 않습니다. 이 결과는 조리 온도가 모형을 개선하지 않는다는 것을 나타냅니다. 이 결과를 토대로 모형에서 조리 온도를 제거하는 것을 고려해 볼 수 있습니다.
