이 항목의 내용
제곱합(SS)
행렬 항에서 여러 제곱합에 대한 공식은 다음과 같습니다.



Minitab에서는 SS 회귀 분석 또는 SS 처리 성분을 순차 제곱합과 수정 제곱합을 모두 사용하여 각 항에 의해 설명되는 변동량으로 세분화합니다.
표기법
| 용어 | 설명 |
|---|---|
| b | 계수의 벡터 |
| X | 설계 행렬 |
| Y | 반응 값의 벡터 |
| n | 관측치 수 |
| J | 1의 n x n 행렬 |
순차 제곱합
Minitab에서는 변동의 SS 회귀 분석 또는 처리 성분을 각 요인의 순차 제곱합으로 세분화합니다. 순차 제곱합은 모형에 요인 또는 예측 변수를 입력한 순서에 따라 다릅니다. 순차 제곱합은 이전에 요인을 입력한 경우 SS 회귀 분석에서 한 요인만으로 설명되는 부분을 나타냅니다.
예를 들어 X1, X2, X3 등 요인 또는 예측 변수가 세 개인 모형의 경우 X2의 순차 제곱합은 X1이 모형에 포함된 상태에서 X2에 의해 설명되는 분산의 정도를 나타냅니다. 요인의 다른 순서를 얻으려면 분석을 반복하고 다른 순서로 요인을 입력합니다.
수정 제곱합
수정 제곱합은 항을 모형에 입력하는 순서에 의존하지 않습니다. 항을 모형에 입력한 순서에 관계없이 다른 모든 항이 주어진 경우 수정 제곱합은 항에 의해 설명되는 변동량입니다.
예를 들어 X1, X2, X3 등 요인이 세 개인 모형의 경우 X2의 수정 제곱합은 X1과 X3에 대한 항도 모형에 포함된 상태에서 X2에 대한 항에 의해 설명되는 분산의 정도를 나타냅니다.
세 요인에 대한 수정 제곱합은 다음과 같이 계산됩니다.
- SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) 또는
- SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)
여기서 SSR(X3 | X1, X2)은 X1과 X2가 모형에 있는 경우 X3에 대한 수정 제곱합입니다.
- SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) 또는
- SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)
여기서 SSR(X3 | X1, X2)은 X1이 모형에 있는 경우 X2와 X3에 대한 수정 제곱합입니다.
모형에 4개 이상의 요인이 있는 경우 이 공식을 확장할 수 있습니다1.
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
자유도(DF)
모형의 각 성분에 대한 자유도는 다음과 같습니다.
| 변동 원인 | DF |
|---|---|
| 요인 | ki – 1 |
| 공변량 및 공변량 간의 교호작용 | 1 |
| 요인이 포함된 교호작용 | 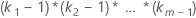 |
| 회귀 분석 | p |
| 오차 | n – p – 1 |
| 합계 | n – 1 |
- 데이터에 예측 변수 값이 같은 여러 개의 관측치가 포함됩니다.
- 데이터에 모형에 없는 추가 항을 추정하기 위한 올바른 점이 포함됩니다.
표기법
| 용어 | 설명 |
|---|---|
| ki | i번째 요인의 수준 수 |
| m | 요인 수 |
| n | 관측치 수 |
| p | 상수를 제외한 모형 내 계수의 수 |
Adj MS – 회귀 분석
회귀 분석의 평균 제곱(MS)에 대한 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
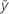 | 평균 반응 |
 | i번째 적합 반응 |
| p | 모형의 항 수 |
Adj MS – 오차
오차의 평균 제곱(MS 오차 또는 MSE로 줄이고 s2로 표기함)은 적합 회귀선 주변의 분산입니다. 공식은 다음과 같습니다.

표기법
| 용어 | 설명 |
|---|---|
| yi | i번째 관측된 반응 값 |
 | ith번째 적합 반응 |
| n | 관측치 수 |
| p | 상수를 제외한 모형 내 계수의 수 |
F
모형의 모든 요인이 고정 요인인 경우 F-통계량은 다음과 같이 가설 검정에 따라 계산됩니다.
- F(항)
-

- F(적합성 결여)
-

모형에 변량 요인이 있는 경우 F는 각 항에 대한 기대 평균 제곱을 사용하여 구성됩니다. 자세한 내용은 Neter et al.1을 참조하십시오.
표기법
| 용어 | 설명 |
|---|---|
| Adj MS 항 | 한 항이 모형의 다른 항을 설명한 후 설명하는 변동량의 측도. |
| MS 오차 | 모형이 설명하지 않는 변동의 측도. |
| MS 적합성 결여 | 모형에 항을 추가하여 모형화할 수 있는 반응의 변동 측도. |
| MS 순수 오차 | 반복된 반응 데이터의 변동 측도. |
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
p-값 – 분산 분석표
p-값은 자유도(DF)가 다음과 같은 F 분포에서 계산되는 확률입니다.
- 분자 DF
- 검정의 항에 대한 자유도의 합
- 분모 DF
- 오차에 대한 자유도
공식
1 − P(F ≤ fj)
표기법
| 용어 | 설명 |
|---|---|
| P(F ≤ f) | F-분포의 누적분포함수 |
| f | 검정에 대한 f-통계량 |
순수 오차 적합성 결여 검정
- 반복실험의 각 집합 내 평균으로부터 반응의 제곱 편차의 합을 계산한 다음 더하여 순수 오차 제곱합(SS PE)을 생성합니다.
- 순수 오차 평균 제곱
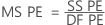

여기서 n = 관측치의 수이고 m = 고유한 x-수준 조합의 수입니다.
- 적합성 결여 제곱합
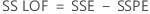
- 적합성 결여 평균 제곱

- 검정 통계량
큰 F-값과 작은 p-값은 모형이 적절하지 않다는 것을 나타냅니다.
p-값 - 적합성 결여 검정
- 분자 DF
- 적합성 결여 검정의 자유도
- 분모 DF
- 순수 오차에 대한 자유도
공식
1 − P(F ≤ fj)
표기법
| 용어 | 설명 |
|---|---|
| P(F ≤ fj) | F-분포의 누적분포함수 |
| fj | 검정에 대한 f-통계량 |
