방법
2-요인 모형의 경우, 평균 분석은 교호작용 효과가 유의한지 또는 주효과가 총 평균과 다른지 여부를 확인하기 위한 절차입니다. 이원 평균 분석의 경우 데이터가 균형적이어야 합니다.
평균
공식
지정된 수준에서 요인에 대한 관측치의 평균입니다. Minitab에서는 각 요인 수준에 대한 평균을 그래프에 표시합니다.
| i번째 수준에서 요인 A의 평균: |
 |
| j번째 수준에서 요인 B의 평균: |
 |
표기법
| 용어 | 설명 |
|---|---|
| yi. | 요인 A의 i번째 수준에 대한 모든 관측치의 합 |
| y.j. | 요인 B의 j번째 수준에 대한 모든 관측치의 합 |
| a | A의 수준 수 |
| b | B의 수준 수 |
| n | 요인 A의 i번째 수준 및 요인 B의 j번째 수준에서 사례의 수 |
총 평균(중심선)
공식
표본 내 모든 관측치의 평균입니다. Minitab에서는 총 평균을 주효과 그래프의 중심선으로 사용합니다.
표기법
| 용어 | 설명 |
|---|---|
| y... | 표본 내 모든 관측치의 합 |
| a | A의 수준 수 |
| b | B의 수준 수 |
| n | 요인 A의 i번째 수준 및 요인 B의 j번째 수준에서 사례의 수 |
주효과에 대한 상위 및 하위 결정 한계
결정 한계는 요인 수준 평균이 총 평균과 다른지 여부를 나타냅니다. 상위 결정 한계(UDL) 또는 하위 결정 한계(LDL)를 벗어나 있는 점은 총 평균과 통계적으로 다릅니다.
상위 및 하위 결정 한계는 요인의 수준 수 및 각 수준에서의 관측치 수에 따라 다르게 계산됩니다. 아래 수식은 요인 A에 대한 상위 및 하위 결정 한계를 표시합니다. 요인 B의 결정 한계를 계산하려면 특정 항을 요인 A에 해당하는 항으로 바꿉니다.
2-수준 요인
요인 A에 대한 상위 및 하위 결정 한계는 다음과 같습니다.
- UDLA =
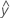...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)] - LDLA =
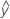...- (.5) * hα* Sqrt[(MSE) * (2/ n1)]
여기서 ha = 절대값(t(a / 2; abn - ab), MSE = (항 A, B, AB를 사용한 분산 분석의) 평균 제곱 오차, n1= 요인 A의 각 수준에서의 관측치 수입니다.
수준이 3개 이상인 요인
- UDLA =
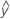...+ hα* Sqrt[MSE * (- 1) / (a * n1)] - LDLA =
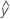...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
여기서 MSE = (항 A, B, AB를 사용한 분산 분석의) 평균 제곱 오차, a = 요인 A의 요인 수준 수, n1= 요인의 각 수준에서의 관측치 수입니다. 임계값 hα는 알파, 표시되는 평균 수 및 MSE의 자유도에 따라 달라집니다. Nelson1의 부록 B에서 표 B.1에서 hα 값을 찾을 수 있습니다.
0.001과 0.1의 범위를 벗어나는 알파 값의 경우, 결정 한계는 다음과 같습니다.
- UDLA =
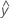...+ hα* Sqrt[MSE * (- 1) / (a * n1)] - LDLA =
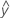...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
여기서 MSE = (항 A, B, AB를 사용한 분산 분석의) 평균 제곱 오차, n1= 요인의 각 수준에서의 총 관측치 수, hα = 절대값(t(α2, df)입니다. a2 = (1- (1- a )** (1 / a)) / 2 및 df = nT - ab이고 nT = 표본의 총 관측치 수입니다.
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
교호작용 효과에 대한 상위 및 하위 결정 한계
결정 한계는 교호작용이 유의한지 여부를 나타냅니다. 상위 결정 한계(UDL) 또는 하위 결정 한계(LDL)를 벗어나 있는 점은 교호작용이 통계적으로 유의하다는 것을 나타냅니다.
아래에는 요인 A와 B의 교호작용에 대한 상위 및 하위 결정 한계의 일반적인 수식입니다. 항은 각 요인의 수준 및 관측치 수에 따라 다르게 정의됩니다.
- UDLAB = hα* Sqrt[MSE * (q / (a * b * n)]
- UDLAB = hα* Sqrt[MSE * (q / (a * b * n)]
여기서 ha = 절대값(t(α2, dfe)), a = 요인 A의 수준 수, b = 요인 B의 수준 수, n = 요인 간 각 교호작용의 관측치 수, q = 교호작용 효과에 대한 자유도, (a - 1)(b - 1) 및 dfe = 오차, abn - ab에 대한 자유도입니다.
요인 A와 B 모두 2개의 수준이 있음
- α2 = a / 2
요인 A에는 2개의 수준이 있고 요인 B에는 3개 이상의 수준이 있음
- α2 = (1- (1- a )** (1 / b)) / 2
여기서 a = 요인 A의 수준 수이고 b = 요인 B의 수준 수입니다.
요인 A에는 3개 이상의 수준이 있고 요인 B에는 2개의 수준이 있음
- α2 = (1- (1- a )** (1 / a)) / 2
여기서 a = 요인 A의 수준 수이고 b = 요인 B의 수준 수입니다.
요인 A와 B 모두 3개 이상의 수준이 있음
- α2 = (1- (1- a )** (1 /a * b)) / 2
여기서 a = 요인 A의 수준 수이고 b = 요인 B의 수준 수입니다.
