장기 및 단기 표준 편차를 추정하기 위한 불편화 상수
- 장기 표준 편차를 추정하기 위한 불편화 상수
-
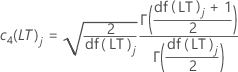
- 단기 표준 편차를 추정하기 위한 불편화 상수
-
설명:
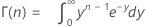
표기법
| 용어 | 설명 |
|---|---|
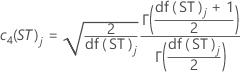
| c4(LT)j | j번째 누적 부분군에서 장기 계산을 위한 불편화 상수 |
| c4(ST)j | j번째 누적 부분군에서 단기 계산을 위한 불편화 상수 |
| df(LT)j | j번째 부분군의 장기 자유도 |
| df(ST)j | j번째 부분군의 단기 자유도 |
단기 표준 편차
- 불편화 상수를 사용한 단기 표준 편차(기본값)
-

- 불편화 상수를 사용하지 않은 단기 표준 편차
-
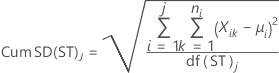
설명:
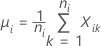
표기법
| 용어 | 설명 |
|---|---|
| Cum SD(ST)j | j번째 부분군까지 누적 단기 표준 편차 |
| c4(ST)j | j번째 누적 부분군에서 단기 계산을 위한 불편화 상수 |
| df(ST)j | j번째 부분군의 단기 자유도 |
장기 표준 편차
- 불편화 상수를 사용하지 않은 장기 표준 편차(기본값)
-
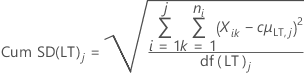
- 불편화 상수를 사용한 장기 표준 편차
-
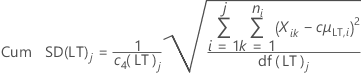
설명:
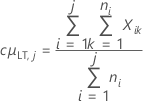
표기법
| 용어 | 설명 |
|---|---|
| Cum SD(LT)j | j번째 부분군까지 누적 장기 표준 편차 |
| c4(LT)j | j번째 누적 부분군에서 장기 계산을 위한 불편화 상수 |
| df(LT)j | j번째 부분군의 장기 자유도 |
장기 공정 평균
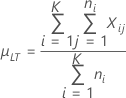
표기법
| 용어 | 설명 |
|---|---|
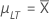
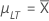
| µLT |
장기 평균 또는 공정 평균 μLT = cμLT,K 참고
|
장기 공정 표준 편차
σLT = Cum SD(LT)K
단기 공정 평균
- 목표값이 주어진 경우
- μST = T
- 두 규격 한계가 모두 주어진 경우(목표값이 주어지지 않음)

- 한 규격 한계가 주어진 경우(목표값이 주어지지 않음)
- μST = μLT
표기법
| 용어 | 설명 |
|---|---|
| µST | 단기 평균 |
| T | 목표 |
| µLT |
장기 평균 또는 공정 평균 참고
|
단기 공정 표준 편차
σST = Cum SD(ST)K
자세한 내용은 Minitab에서 공정 보고서의 단기 통계량을 위한 중심화 값을 선택하는 방법에서 확인하십시오.
공정 능력 통계량
- CCpk
-

- Cp
-

- Cpk
-
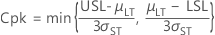
- CPL
-

- CPU
-

참고
Cp, Cpk 및 CCpk는 공정의 잠재적인 공정 능력을 나타냅니다. 따라서 이러한 공식에서는 단기 변동성을 사용합니다.
- Pp
-

- Ppk
-
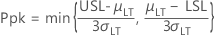
- PPL
-
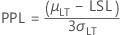
- PPU
-

참고
Pp와 Ppk는 실제 공정 성능을 나타냅니다. 따라서 이러한 공식에서는 장기 변동성을 사용합니다.
자유도
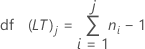
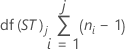
표기법
| 용어 | 설명 |
|---|---|
| df(LT)j | j번째 부분군의 장기 자유도 |
| df(ST)j | j번째 부분군의 단기 자유도 |
확률
- P.LSL(LT)j
-
j번째 부분군에서 규격 하한보다 작거나 같은 장기 확률
P.LSL(LT) j = 1 – Φ(Z.LSL(LT)j)
- P.LSL(ST) j
-
j번째 부분군에서 규격 하한보다 작거나 같은 단기 확률
P.LSL(ST) j = 1 – Φ(Z.LSL(ST)j)
- P.USL(LT) j
-
j번째 부분군에서 규격 상한보다 크거나 같은 장기 확률
P.USL(LT) j = 1 – Φ(Z.USL(LT)j)
- P.USL(ST) j
-
j번째 부분군에서 규격 상한보다 크거나 같은 단기 확률
P.USL(ST) j = 1 – Φ(Z.LSL(ST)j)
- P.Total(LT) j
-
j번째 부분군에서 규격을 벗어나는 전체(장기) 확률
P.Total(LT) j = P.USL(LT)j + P.LSL(LT)j
- P.Total(ST)j
-
j번째 부분군에서 규격을 벗어나는 전체(단기) 확률
P.Total(ST)j = P.USL(ST)j + P.LSL(ST)j
Z.bench 통계량
- Z.Bench(LT)j
-
j번째 부분군의 벤치마크 Z(장기)
Z.Bench(LT)j = Φ−1(P.Total(LT)j)
- Z.Bench(ST)j
-
j번째 부분군의 벤치마크 Z(단기)
Z.Bench(ST)j = Φ−1(P.Total(ST)j)
- Z.LSL(LT)j
-
j번째 부분군에서 규격 하한의 Z 값(장기)
Z.LSL(LT)j = (μLT – LSL) / Cum SD(LT)j
- Z.LSL(ST)j
-
j번째 부분군에서 규격 하한의 Z 값(단기)
Z.LSL(ST)j = (μST – LSL) / Cum SD(ST)j
- Z.USL(LT)j
-
j번째 부분군에서 규격 상한의 Z 값(장기)
Z.USL(LT)j = (USL – μLT) / Cum SD(LT)j
- Z.USL(ST)j
-
j번째 부분군에서 규격 상한의 Z 값(단기)
Z.USL(ST)j = (USL – μST) / Cum SD(ST)j
- Z.Shiftj
-
j번째 부분군의 이동 요인
Z.Shiftj = Z.Bench(ST)j – Z.Bench(LT)j