공정 보고서에 대한 모든 공정 능력 보고서

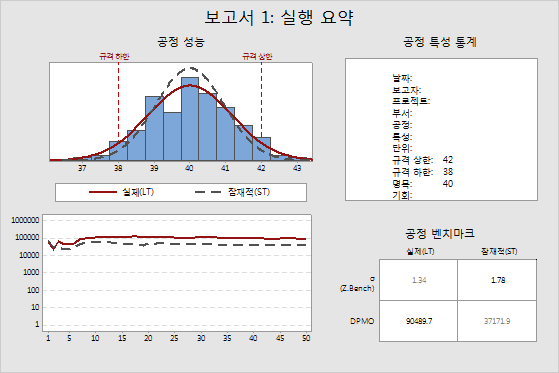
공정 성능 상단 그림: 정적 공정 성능 LT/ST

히스토그램의 정규 곡선이 프로젝트 CTQ 측정값의 추정된 분포를 나타냅니다. CTQ(핵심 품질 요소)는 고객을 만족시키기 위해 성능 표준을 충족해야 하는, 제품 또는 공정의 일차적으로 측정 가능한 특성을 가리킵니다. CTQ에는 제품 또는 서비스와 관련된 변수 및 규격 상한과 하한이 포함될 수 있습니다.

Minitab에서는 공정 평균과 공정 표준 편차의 장기(LT) 및 단기(ST) 추정치로부터 이러한 곡선을 계산합니다. 그런 다음 LT 정규 곡선과 ST 정규 곡선을 그립니다. 대부분 LT 정규 곡선이 ST 정규 곡선보다 폭이 넓습니다.

규격 한계(LSL과 USL)가 기준 점을 제공합니다. 목표값(명목 값)은 항상은 아니지만 일반적으로 대부분 규격 하한과 규격 상한의 중간에 위치합니다. 이상적으로 평균은 목표값에 가까워야 합니다. 위의 예에서 공정 평균은 목표값에 매우 가까운 것으로 보입니다.

공정 성능 하단 그림: 동적 공정 성능 LT/ST

이 그림에는 LT(장기) 및 ST(단기)의 경우 모두 데이터의 각 부분군 다음에 추정된 누적 DPMO(백만 번 기회당 결점 수)가 표시됩니다. Minitab에서는 먼저 각 부분군 다음에 Z.Bench를 얻는 방식으로 DPMO를 계산한 후 해당 값을 DPMO로 변환합니다. LT와 ST의 경우 모두 Z.Bench 값은 추정된 평균과 표준 편차의 함수입니다.

공정이 안정적인 경우 이 그림의 선들은 일정한 값에 가까워집니다. 선들이 안정되지 않으면 공정이 안정적이지 않거나 데이터가 충분하지 않은 것입니다. 위의 예에서는 두 선 모두 그림의 왼쪽에서는 변동하지만 그림의 오른쪽에서는 안정됩니다. 선들이 그림의 왼쪽에서 상대적으로 평평하면 일정하게 증가 또는 감소합니다. 이것은 평균이 이동하거나 공정 변동이 변경되거나 공정에서 무언가 변경되었음을 나타냅니다. 대부분의 경우 공정 변동의 영향으로 인해 LT Z.Bench가 ST Z.Bench보다 작기 때문에 LT 선이 ST 선보다 위에 있습니다.

이 그림의 두 선 모두 부분군이 몇 개 있는 왼쪽에서는 위아래로 변동되어야 하지만, 충분한 데이터가 수집되고 공정이 안정적인 경우 오른쪽에서는 안정되어야 합니다. 선들이 안정되지 않는 경우 "보고서 4: 누적 통계량"에서 데이터가 충분하지 않은 것이 문제인지 공정의 불안정성이 문제인지 여부를 확인할 수 있습니다.

공정 특성 통계

특성 통계표에는 사용자가 지정한 프로젝트 정보와 공정 정보가 표시됩니다.

공정 벤치마크

굵게 표시된 숫자는 ST 시그마(또는 Z.Bench)와 LT DPMO입니다. 대부분의 Black Belt에서는 이 두 값을 사용하여 공정 성능을 보고합니다.

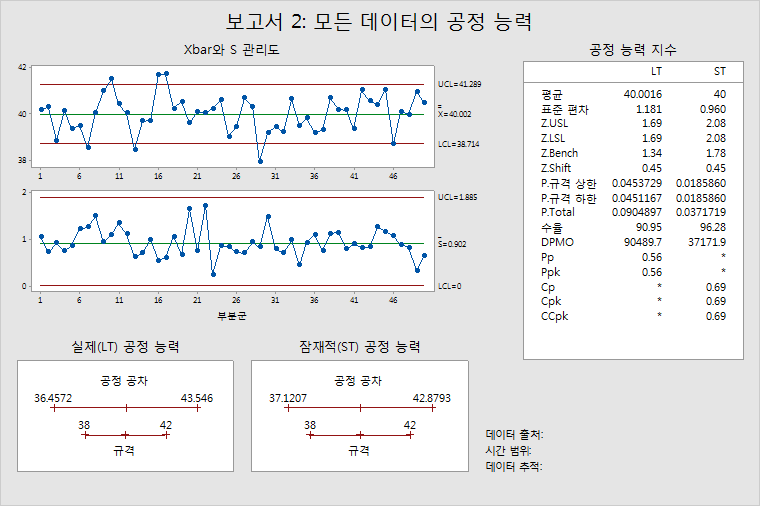
공정 데이터의 관리도

데이터가 수집되었을 때의 공정 안정성을 표시합니다. 1보다 큰 부분군의 경우 Xbar 관리도를 사용하여 공정 평균의 안정성을 확인하고 S 관리도를 사용하여 공정 표준 편차의 안정성을 확인할 수 있습니다. 부분군 크기 = 1인 경우 Minitab에서는 I 관리도와 MR 관리도를 표시합니다.

공정 능력 그림 LT/ST

규격 한계에 상대적인 추정된 공정 공차를 표시합니다. 공정 공차는 공정 중심 점 ± 3 표준 편차입니다. LT와 ST의 공정 중심 점과 공정 표준 편차가 다르기 때문에 두 개의 그림이 있습니다. LT는 공정 평균을 중심 점으로 사용하고 ST는 목표값(또는 규격 한계의 중간점, 하나의 규격 한계만 지정되는 경우에는 공정 평균)을 중심 점으로 사용합니다. 자세한 내용은 Minitab에서 공정 보고서의 단기 통계량을 위한 중심화 값을 선택하는 방법에서 확인하십시오.

다시 말하면 이 그래프는 자동차(공정)가 차고(규격)에 들어 맞는지 여부 또는 자동차가 차고를 향하고 있는지 여부를 나타냅니다. 위의 예에서 공정은 규격보다 폭이 넓습니다. 그러나 공정은 공정 중심 점(평균)이 목표값과 거의 동일하게 표시되는 LT 그림에서처럼 중심화됩니다.

공정 능력 지수 LT/ST

공정 성능을 보고하기 위해 일반적으로 사용되는 통계량을 표시합니다. 장기(LT) 및 단기(ST) 성능을 측정하는 통계량의 비교에 대한 내용은 공정 능력 측정 기준의 이해를 참조하십시오.

공정 성능을 설명하려면 Z.Bench 값을 사용합니다. Z.Bench 통계량은 적절한 공정 조건을 바탕으로 하지만 결점 확률의 추정치, PPM, DPMO 등으로도 직접 이어집니다. Z.Bench 통계량과 같은 공정 조건을 바탕으로 하는 CCpk 및 Ppk을 대신 사용할 수도 있습니다.

특정 계산에 대한 자세한 내용은 공정 보고서에 대한 공정 통계량 및 공정 능력 값 계산에서 확인하십시오.

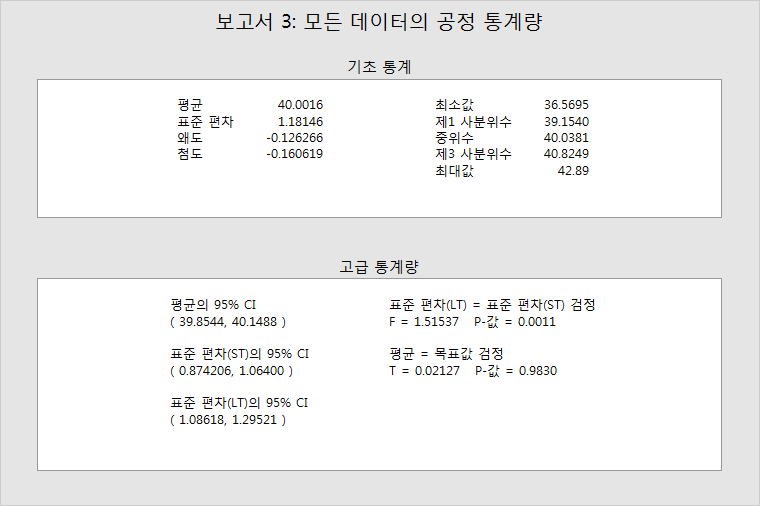
기초 통계

이 표는 공정 평균(LT 평균), 공정 표준 편차(LT 표준 편차) 및 기타 기초 통계량을 제공합니다.

데이터가 정규 분포를 따르는지 여부를 확인하려면 왜도와 첨도를 사용합니다. 그러나 확률도가 훨씬 더 유용합니다. (보고서 6에서 정규 확률도는 결점의 확률을 추정합니다.)

최소값, 제1 사분위수, 중위수, 제3 사분위수 및 최대값이 데이터의 산포도를 보여줍니다. 예를 들어, 데이터의 25%는 39.1540(제1 사분위수)보다 크지 않고, 데이터의 50%는 40.0381(중위수)보다 크지 않으며, 데이터의 75%는 40.8249(제3 사분위수)보다 크지 않습니다.

고급 통계량

이 표는 공정 모수, ST 평균 및 표준 편차에 대한 통계적 추론을 제공합니다.

공정 평균에는 공정 평균이 공정 목표값과 같은지 여부를 보여주는 95% 신뢰 구간 및 검정 통계량이 포함됩니다. 공정 평균과 공정 목표값 사이에 통계적으로 유의한 차이가 없을 경우 p-값은 0.05보다 크고 공정 목표 값은 신뢰 구간의 한계 내에 포함됩니다. 위의 예에서 검정의 p-값은 0.983이고 목표값(40)은 평균에 대한 95% 신뢰 구간의 한계 내에 포함됩니다. 따라서 공정 평균이 공정 목표값과 같다는 귀무 가설을 기각할 수 없습니다.

이 표는 또한 LT 및 ST 표준 편차 모두에 대한 95% 신뢰 구간 및 이들 두 값이 같은지 여부를 확인할 수 있는 검정을 제공합니다. LT와 ST 공정 표준 편차 사이에 통계적으로 유의한 차이가 없을 경우, 공정에 유의한 변동이 없으며 데이터가 수집될 때 특수 원인이 존재하지 않았다는 결론을 내릴 수 있습니다. 위의 예에서 등분산 검정의 p-값은 0.0011입니다. 따라서 귀무 가설을 기각하고 LT 표준 편차와 ST 표준 편차가 유의하게 다르다는 결론을 내려야 합니다.

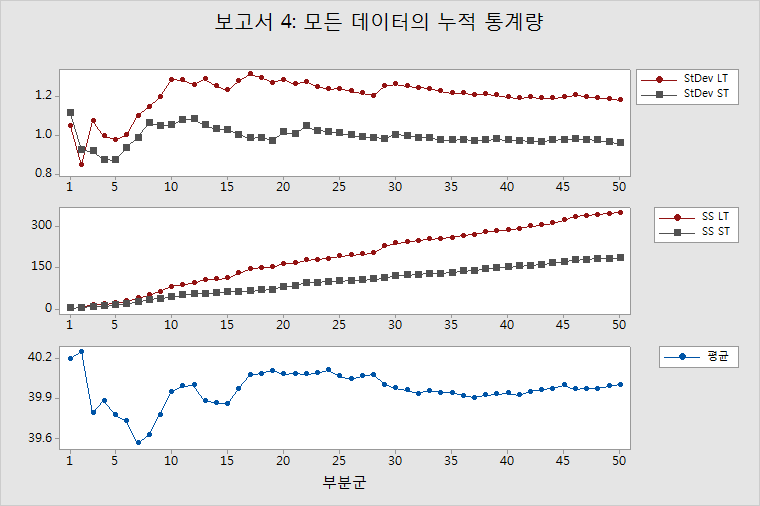
누적 표준 편차 LT/ST

이 그림은 데이터의 각 부분군 뒤에 LT 표준 편차와 ST 표준 편차의 추정치를 모두 표시합니다. 공정 성능의 모든 측정 기준이 공정 표준 편차의 추정치를 바탕으로 하므로, 이러한 추정치가 적절한지 여부를 결정해야 합니다. 추정치가 적절한지 여부는 안정된 공정(내재되어 있는 변동성이 변화하지 않는 공정) 및 공정을 특성화하기에 충분한 데이터에 달려 있습니다.

LT 표준 편차와 ST 표준 편차의 추정치는 부분군이 몇 개 포함된 그림의 왼쪽에서 상당히 진동해야 합니다. 공정이 안정되고 충분한 데이터를 수집한 경우 추정치는 그림의 오른쪽에서 안정됩니다. 그림의 선들이 계속해서 진동한다면 충분한 데이터를 수집하지 않았거나 공정 변동이 불안정하기 때문입니다.

안정된 공정의 경우에는 LT 표준 편차와 ST 표준 편차 간의 차이가 상당히 일정해야 합니다. 평균이 이동하거나 분산이 변화하는 경우와 같이 공정이 변화하는 경우 LT 표준 편차와 ST 표준 편차 간의 차이도 변화합니다.

자세한 내용은 공정 보고서을 사용하여 공정 평균 이동 확인 및 공정 보고서을 사용하여 공정 변동성의 증가 확인에서 확인하십시오.

누적 제곱합 LT/ST

이 그림은 데이터의 각 부분군 뒤에 편차 제곱의 합(총 제곱합 또는 제곱합 LT)과 각 부분군 내 모든 편차 제곱의 합(군내 제곱합 또는 제곱합 ST)을 모두 표시합니다. 자세한 내용은 공정 보고서에 대한 제곱합 계산에서 확인하십시오.

제곱합 ST는 공정에 내재된 변동의 변화를 탐지하기 위한 매우 유용한 진단 도구입니다. 내재된 변동이 안정적인 경우 각 부분군의 군내 제곱합은 거의 같습니다. 따라서 각 부분군의 제곱합 ST는 거의 같은 양만큼 증가해야 하며 그 결과 위쪽 방향으로 기울기가 일정한 제곱합 ST 선이 표시됩니다. 공정에 내재된 변동성이 변화하면 제곱합 ST 선의 기울기가 달라집니다.

총 제곱합은 군내 제곱합과 군간 제곱합의 합입니다. 그러므로, 공정 분산과 공정 평균 둘 다의 안정성의 영향을 받습니다. 둘 다 안정적인 경우 총 제곱합에 대한 기여도는 각 부분군에 대해 거의 같습니다. 따라서 각 부분군의 제곱합 LT는 거의 같은 양만큼 증가해야 하며 그 결과 위쪽 방향으로 기울기가 일정한 제곱합 LT 선이 표시됩니다. 공정에 내재된 변동성이 변화하면 제곱합 LT 선의 기울기가 달라집니다.

내재된 공정 변동성이 갑자기 변화하면 군내 제곱합과 군간 제곱합에 모두 영향을 미치며, 제곱합 ST와 제곱합 LT 선의 기울기가 모두 달라집니다. 따라서 두 선의 기울기가 달라지면 내재된 공정 변동성에 변화가 있다는 것을 나타냅니다.

공정 평균의 이동은 군간 제곱합에 영향을 미치지만 군내 제곱합에는 영향을 미치지 않습니다. 따라서 제곱합 LT 선의 기울기는 달라지지만 제곱합 ST 선의 기울기는 달라지지 않습니다. 즉, 제곱합 LT 선의 기울기는 달라지지만 제곱합 ST 선의 기울기는 달라지지 않으면 공정 평균에 이동이 있다는 것을 나타냅니다.

자세한 내용은 공정 보고서을 사용하여 공정 평균 이동 확인 및 공정 보고서을 사용하여 공정 변동성의 증가 확인에서 확인하십시오.

누적 평균

이 그림은 각 부분군 뒤에 공정 평균의 추정치를 표시합니다. 공정 평균의 추정치가 적절한지 여부는 수집한 데이터의 양과 공정의 안정성에 따라 결정됩니다.

추정치는 부분군이 몇 개 포함된 그림의 왼쪽에서 위아래로 상당히 진동해야 합니다. 공정이 안정되고 충분한 데이터를 수집한 경우 추정치는 그림의 오른쪽에서 안정됩니다. 선들이 계속해서 진동한다면 충분한 데이터를 수집하지 않았거나 공정 평균이 크게 흔들리기 때문입니다. 데이터가 충분하지 않은 것이 문제인지 여부를 확인하려면 누적 표준 편차 그림을 확인하십시오. 데이터가 충분하지 않은 경우 LT와 ST 선도 진동합니다.

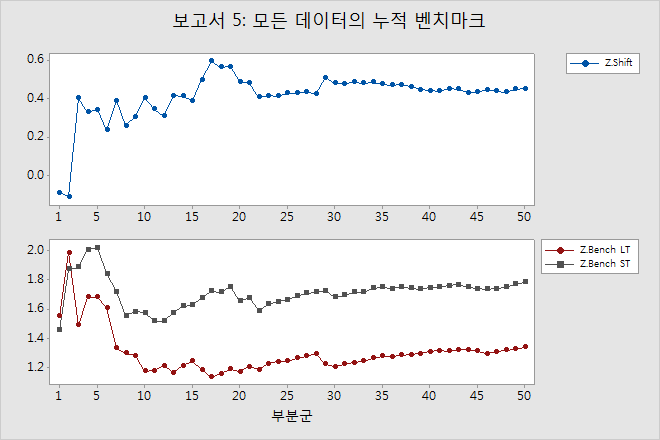
Z.Shift

Z.Shift는 Z.Bench LT와 Z.Bench ST 간의 간격과 같습니다.

이 그림의 선은 부분군이 몇 개 포함된 왼쪽에서는 위아래로 진동해야 하지만, 충분한 데이터를 수집하고 공정이 안정적인 경우 오른쪽에서는 안정되어야 합니다.

Z.Bench LT 및 Z.Bench ST

Z.Bench 그림은 이 통계량을 사용하여 공정 성능을 확실히 보고하기에 충분한 데이터가 수집되었는지 여부를 나타냅니다. 이 그림의 두 선은 모두 부분군이 몇 개 포함된 왼쪽에서 위아래로 진동해야 하지만, 충분한 데이터를 수집하고 공정이 안정적인 경우 오른쪽에서 안정되어야 합니다. 선들이 안정되지 않은 경우에는 누적 통계량 보고서의 그림이 데이터가 충분하지 않은 것이 문제인지 공정의 불안정성이 문제인지 여부를 확인하는 데 도움이 됩니다.

Z.Bench 그림의 차이와 Z.Shift 그림의 선은 모두 위의 예와 같이 일정한 값에 가까워져야 합니다.

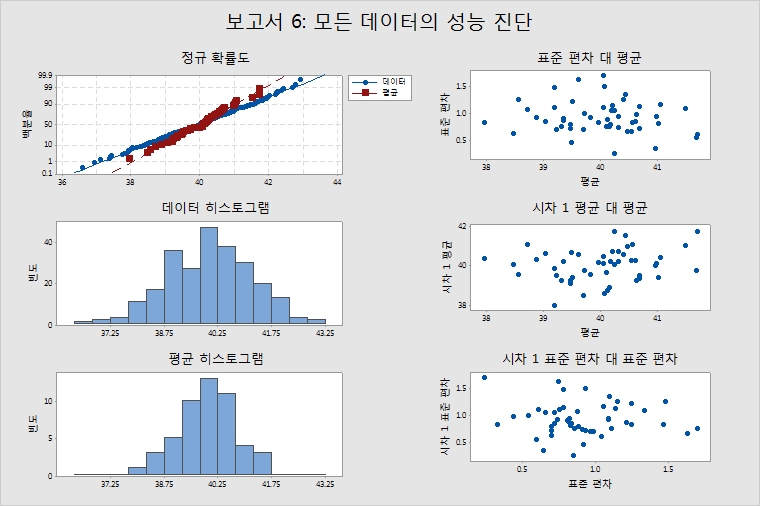
정규 확률도, 히스토그램 및 평균 히스토그램

이 그림은 데이터가 정규 분포를 따르는지 여부를 확인하는 데 도움이 됩니다. 데이터가 정규 분포를 따르지 않을 경우 결점 확률의 추정치(예: DPMO)는 정확하지 않습니다. 대부분의 경우 이 추정치는 실제 값보다 작은 경향이 있습니다. 따라서 DPMO와 같은 추정치를 사용하기 전에 정규 확률도 및 두 개의 히스토그램을 통해 데이터가 정규 분포를 따르는지 여부를 확인하십시오. 위 예의 데이터는 정규 분포를 따르는 것으로 보입니다.

데이터의 치우침이 심한 경우에는 Box-Cox 변환과 같은 변환을 실행하여 문제를 수정하십시오. 다음 값과 함께 Box-Cox 누승 변환(W=Y^λ) 사용(공정 보고서 옵션 하위 대화 상자)을 선택하면 Minitab이 데이터, 목표값, 규격 한계를 자동으로 변환합니다. 그러나 데이터를 수동으로 변환하는 경우에는 목표값과 규격 한계도 수동으로 변환해야 합니다.

표준 편차 대 평균

부분군 평균과 부분군 표준 편차 사이에 아무런 상관 관계도 없을 경우 이 그림에는 위 예와 같이 랜덤하게 흩어진 점들이 표시되어야 합니다.

평균과 표준 편차 사이에 양의 상관 관계가 있을 경우 부분군 평균이 증가하면 부분군 표준 편차가 증가하는 경향이 있습니다. Box-Cox 변환(λ = 0)은 이러한 경우 일반적으로 효과가 있는 잘 알려진 분산 안정화 변환입니다.

시차 1 평균 대 평균

시차 1 평균 대 평균의 그림은 (부분군 평균)_i 대 (부분군 평균)_i–1의 그림입니다. 이 그림에는 위 예와 같이 연속적인 부분군 평균 사이에 아무런 상관 관계도 없다는 것을 나타내는, 랜덤하게 흩어진 점들이 표시되어야 합니다.

양의 상관 관계가 있고 한 부분군 평균이 전체 공정 평균보다 큰 경우, 다음 부분군 평균도 전체 공정 평균보다 클 가능성이 많습니다. 따라서 양의 상관 관계는 공정 평균에 변동이 발생하기 쉽다는 것을 의미합니다. 상관 관계가 음이면 연속적인 두 개의 낮은 부분군 평균이 아니라 교대로 상승, 하강하는(낮음, 높음, 낮음) 부분군 평균을 나타냅니다. 음의 상관 관계는 공정이 지나치게 제어되고 있다는 것을 나타냅니다.

시차 1 표준 편차 대 표준 편차

시차 1 표준 편차 대 표준 편차의 그림은 (부분군 표준 편차)_i 대 (부분군 표준 편차)_i–1의 그림입니다. 이 그림에는 연속적인 부분군 표준 편차 사이에 아무런 상관 관계도 없다는 것을 나타내기 위해 위 예와 같이 랜덤하게 흩어진 점들이 표시되어야 합니다.

부분군 평균과 마찬가지로, 양의 상관 관계가 있고 한 부분군의 표준 편차가 모든 부분군의 평균 표준 편차보다 큰 경우, 다음 부분군의 표준 편차도 모든 부분군의 평균 표준 편차보다 클 가능성이 많습니다. 따라서 부분군 표준 편차는 위아래로 변동하는 경향이 있습니다. 또한 평균도 위아래로 진동하고 부분군 평균과 부분군 표준 편차 사이에 상관 관계가 있을 수 있습니다. 이 경우에는 Box-Cox 변환(λ = 0)을 실행해 보십시오.

부분군 표준 편차에 있어 양의 자기 상관은 공정 내 도구 마모나 기타 감소(지속적인 변동을 초래) 또는 변동에 영향을 미치는 제어되지 않는 장애 요인(예: 상대 습도)의 존재로 인해 야기될 수 있습니다.