평균 풀 할당
수정된 평균은 다음과 같이 계산합니다.
μadj,i = μi + qiμPool
설명:
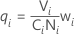
평균 이동 요인을 지정하지 않을 경우 평균 풀 = 0입니다.
분산 풀 할당
수정된 표준 편차는 다음과 같이 계산합니다.
σ2adj,i = σ2i + riσ2Pool
설명:
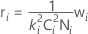
변동 확장 요인을 지정하지 않고 간격 규격 한계를 둘 다 지정하지 않을 경우 분산 풀 = 0입니다.
표기법
| 용어 | 설명 |
|---|---|
| Ci | i번째 원소의 직경 수정 |
| Di | i번째 원소의 표류 요인 |
| Ni | i번째 원소의 복잡도 |
| Si | i번째 원소의 이동 요인 |
| σi | i번째 원소의 표준 편차 |
| σadj,i | i번째 원소의 수정된 표준 편차 |
| T | 간격 목표값(사용할 수 없는 경우 T = μGap,ST) |
| Ti | i번째 원소의 명목 값 |
| μi | i번째 원소의 평균 |
| μadj,i | i번째 원소의 수정된 평균 |
| Vi | i번째 원소의 방향 벡터 |
| wi | 평균 풀 또는 분산 풀에 대한 할당 가중치, i번째 원소 |
| Z.BenchGap,LT | 간격의 벤치마크 Z(장기) |
| Z.BenchGap,ST | 간격의 벤치마크 Z(단기) |
| Z.Benchi,LT | i번째 원소의 벤치마크 Z(장기) |
| Z.Benchi,ST | i번째 원소의 벤치마크 Z(단기) |
| ZP | 장기 간격 분포에 대해 원하는 PPM(오른쪽 꼬리)을 제공하는 Z-값 |
