한 품질 엔지니어가 회사에서 제조하는 전구의 수명을 평가하려고 합니다. 엔지니어는 전구 100개의 랜덤 표본을 수집하여 고장 발생 시까지의 연소 시간을 기록합니다. 엔지니어는 공차 하한(모든 전구의 95% 이상이 초과하는 연소 시간)을 계산하려고 합니다.
- 표본 데이터를 엽니다 전구연소시간.MWX.
- 을 선택합니다.
- 드롭다운 리스트에서 하나 이상의 표본, 한 열에 하나씩을 선택한 다음 시간을 입력합니다.
- 옵션을(를) 클릭합니다.
- 공차 구간에서 하한을 선택합니다.
- 각 대화 상자에서 확인을 클릭합니다.
결과 해석
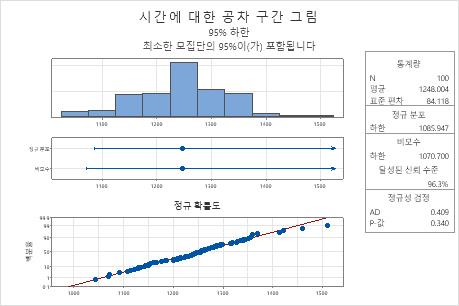
정규 확률도는 표시된 점들이 대략 직선을 이룬다는 것을 보여주며, 이는 데이터가 정규 분포를 따른다는 것을 나타냅니다. 또한 정규성 검정의 p-값은 0.340으로, 유의 수준(α = 0.05)보다 큽니다. 따라서 데이터가 정규 분포를 따르지 않는다는 결론을 내릴 만한 충분한 증거가 없습니다. 엔지니어는 정규 방법 결과를 사용할 수 있습니다.
정규 하한이 1085.94이므로, 엔지니어는 모든 전구의 95% 이상이 약 1086시간의 연소 시간을 초과한다고 95% 신뢰합니다. 모든 전구에 대해 평균 연소 시간은 약 1248시간이며 표준 편차는 약 84.1입니다.
방법
| 신뢰 수준 | 95% |
|---|---|
| 구간 내 모집단의 비율 | 95% |
통계량
| 변수 | N | 평균 | 표준 편차 |
|---|---|---|---|
| 시간 | 100 | 1248.004 | 84.118 |
95% 공차 하한
| 변수 | 정규 방법 | 비모수 방법 | 달성된 신뢰 수준 |
|---|---|---|---|
| 시간 | 1085.947 | 1070.700 | 96.3% |