원하는 방법 또는 공식을 선택하십시오.
최대우도 추정치
분포 모수의 최대우도 추정치는 모수와 관련된 우도 함수를 최대화하여 계산됩니다. 주어진 데이터 집합에 대해 최대 우도 추정치는 분포 모수가 될 수 있는 가능성이 가장 높은 값입니다.
Newton-Raphson 알고리즘은 분포 모수의 최대우도 추정치를 계산하기 위해 사용됩니다. Newton-Raphson 알고리즘은 함수의 최대값을 계산하기 위한 반복적 방법입니다. 1
참고
Minitab에서는 로그 정규 분포를 제외한 모든 분포에 대해 최대우도 방법을 사용하여 모수 추정치를 계산합니다. 로그 정규 분포의 경우에는 불편화 모수 추정치를 계산합니다.
확률 분포
로그 정규 분포
 |
|
| CDF |
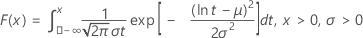 |
| 평균 |
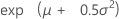 |
| 표준 편차 |
 |
| 용어 | 설명 |
|---|---|
| μ | 척도 모수 |
| σ | 형상 모수 |
감마 분포
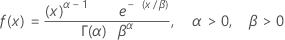 |
|
| CDF |
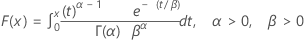 |
| 평균 | αβ |
| 표준 편차 | αβ2 |
| 용어 | 설명 |
|---|---|
| α | 형상 모수 |
| β | 척도 모수 |
지수 분포
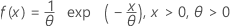 |
|
| CDF |
 |
| 평균 | θ |
| 표준 편차 | θ |
| 용어 | 설명 |
|---|---|
| θ | 척도 모수 |
최소 극단값 분포
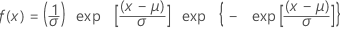 |
|
| CDF |
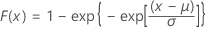 |
| 평균 |
 |
| 표준 편차 |
 |
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
| γ | Euler 상수(대략 0.5772와 같음) |
Weibull 분포
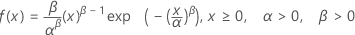 |
|
| CDF |
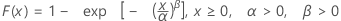 |
| 평균 |
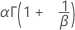 |
| 표준 편차 |
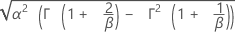 |
| 용어 | 설명 |
|---|---|
| α | 척도 모수 |
| β | 형상 모수 |
최대 극단값 분포
 |
|
| CDF |
 |
| 평균 |
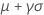 |
| 표준 편차 |
 |
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
| γ | Euler 상수(대략 0.5772와 같음) |
로지스틱 분포
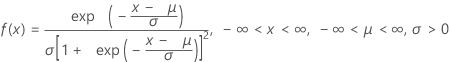 |
|
| CDF |
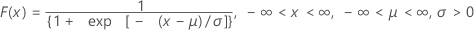 |
| 평균 | μ |
| 표준 편차 |
 |
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
로그 로지스틱 분포
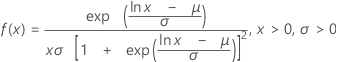 |
|
| CDF |
 |
| 평균 |
 |
| 표준 편차 |
 |
| 용어 | 설명 |
|---|---|
| μ | 위치 모수 |
| σ | 척도 모수 |
1 W. Murray, Ed. (1972). Numerical Methods for Unconstrained Optimization. Academic Press.
