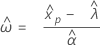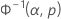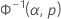확률도
확률도에는 다음이 포함됩니다.
- 점 - 순서가 있는 데이터 집합의 해당 확률에 대한 추정 백분위수입니다.
- 중간선 - 최대우도 모수 추정치를 기반으로 하는 분포의 기대 백분위수입니다. 해당 분포가 데이터에 적합하면 점들은 중간선을 따릅니다.
추정 확률
Minitab에서는 다음과 같은 방법을 사용하여 표시 점을 계산하기 위해 사용되는 확률(P)을 추정합니다.
- 중위수 순위(Benard의 방법)
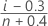
- 평균 순위(Herd-Johnson 추정치)
- 수정된 Kaplan-Meier(Hazen)
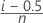
- Kaplan-Meier 제품 한계 추정치
표기법
| 용어 | 설명 |
|---|---|
| n | 관측치 수 |
| i | i번째 관측치 x(i)의 순서, 여기서 x(1), x(2),...x(n)은 순서 통계량 또는 가장 작은 값에서 가장 큰 값의 순서로 정렬된 데이터입니다. |
표시점
확률도의 중간선은 이 표의 x 및 y 좌표 계산을 사용하여 구성됩니다.
| 분포 | x 좌표 | y 좌표 |
|---|---|---|
| 최소 극단값 분포 | x | ln(–ln(1 – p)) |
| 최대 극단값 분포 | x | ln(–ln p) |
| Weibull 분포 | ln(x) | ln(–ln(1 – p)) |
| 3-모수 Weibull 분포 | ln(x – 분계점) | ln(–ln(1 – p)) |
| 지수 분포 | ln(x) | ln(–ln(1 – p)) |
| 2-모수 지수 분포 | ln(x – 분계점) | ln(–ln(1 – p)) |
| 정규 분포 | x | Φ–1기준 |
| 로그 정규 분포 | ln(x) | Φ–1기준 |
| 3-모수 로그 정규 분포 | ln(x – 분계점) | Φ–1기준 |
| 로지스틱 분포 | x |
 |
| 로그 로지스틱 분포 | ln(x) |
 |
| 3-모수 로그 로지스틱 분포 | ln(x – 분계점) |
 |
| 감마 분포 | x | Φ–1감마 |
| 3-모수 감마 분포 | ln(x – 분계점) | Φ–1감마 |
참고
표시점은 분포에 따라 달라지지 않으므로 모든 확률도에 대해 변환 전과 동일하게 됩니다. 그러나 적합선은 선택한 모수 분포에 따라 달라집니다.
표기법
| 용어 | 설명 |
|---|---|
| p | 추정된 확률 |
| Φ-1기준 | 표준 정규 분포의 경우 역 CDF에서 p에 대해 반환된 값 |
| Φ-1감마 | 불완전 감마 분포의 경우 역 CDF에서 p에 대해 반환된 값 |
| ln(x) | x의 자연 로그 |
백분위수 및 백분위수의 표준 오차
백분위수는 척도 100의 값으로, 분포에서 해당 값 이하의 백분율을 나타냅니다. 기본적으로 Minitab에서는 일반적인 백분위수에 대한 모수 분포 분석에 사용할 백분위수의 표를 표시합니다.
백분위수 추정치에 대한 표준 오차는 분산의 제곱근입니다.
, 
, 
, 
, 
, 
, 
, 
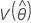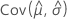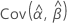및 
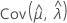는 Fisher 정보 행렬의 역행렬의 적절한 요소에서 가져온 μ, σ, α, β, λ 및 θ의 MLE의 분산 및 공분산을 나타냅니다.
백분위수 및 분산 추정치에 사용되는 공식은 다음과 같습니다.
최소 극단값 분포
- 백분위수
-
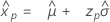
- 분산
-
최대 극단값 분포
- 백분위수
-
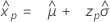
- 분산
-
Weibull 분포
- 백분위수
-
- 분산
-
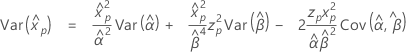
3-모수 Weibull 분포
- 백분위수
-
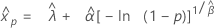
- 분산
-
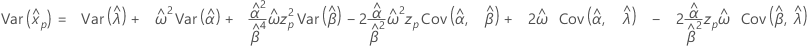
지수 분포
- 백분위수
-
- 분산
-
2-모수 지수 분포
- 백분위수
-
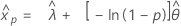
- 분산
-
정규 분포
- 백분위수
-
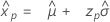
- 분산
-
로그 정규 분포
- 백분위수
-
- 분산
-
3-모수 대수 정규 분포
- 백분위수
-
- 분산
-
로지스틱 분포
- 백분위수
-
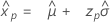
- 분산
-
로그 로지스틱 분포
- 백분위수
-
- 분산
-
3-모수 로그 로지스틱 분포
- 백분위수
-
- 분산
-
감마 분포
- 백분위수
-
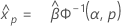
- 분산
-
-
설명
는 정규화된 불완전 감마 분포의 역함수입니다.
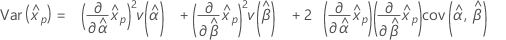
3-모수 감마 분포
- 백분위수
-
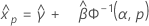
- 분산
-
-
설명
는 정규화된 불완전 감마 분포의 역함수입니다.
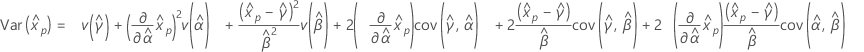
백분위수에 대한 신뢰 한계
| 분포 | 신뢰 한계 |
|---|---|
| 최소 극단값 분포 |
 |
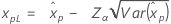| 최대 극단값 분포 |
 |
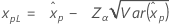| 정규 분포 |
 |
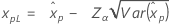| 로지스틱 분포 |
 |
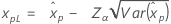| Weibull 분포 |
 |
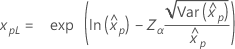| 지수 분포 |
 |
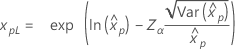| 로그 정규 분포 |
 |
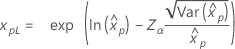| 로그 로지스틱 분포 |
 |
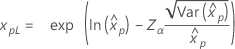| 3-모수 Weibull 분포 |
λ < 0인 경우:
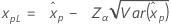 λ ≥ 0인 경우:
  |
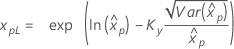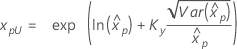| 2-모수 지수 분포 |
λ < 0인 경우:
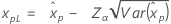 λ ≥ 0인 경우:
  |
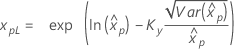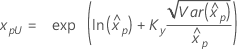| 3-모수 로그 정규 분포 |
λ < 0인 경우:
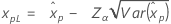 λ ≥ 0인 경우:
  |
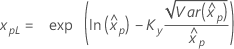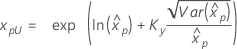| 3-모수 로그 로지스틱 분포 |
λ < 0인 경우:
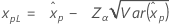 λ ≥ 0인 경우:
  |
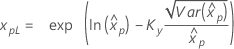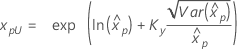표기법
| 용어 | 설명 |
|---|---|
| Kγ | 표준 정규 분포의 (1 + γ) / 2 백분위수 |
