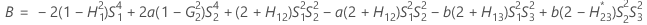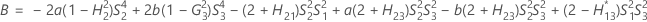이 항목의 내용
반복성 분산 및 총 분산의 비율에 대한 신뢰 구간
두 가지 가능한 계산 방법이 있습니다. Minitab에서는 수정된 대표본(MLS) 방법을 사용하여 한계를 계산합니다. 계산하는 동안 특정 조건이 충족되지 않는 경우, Minitab에서는 Satterthwaite 근사를 사용합니다. 단측 신뢰 한계를 계산하려면 H 및 G에서 α/2를 α로 대치하십시오.
MLS 방법


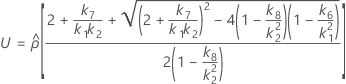
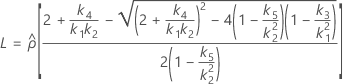
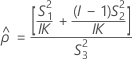
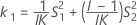
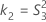
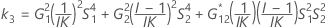
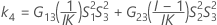

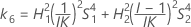
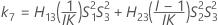

MLS 방법을 사용한 하한과 상한의 존재에 대한 두 가지 조건은 다음과 같습니다.
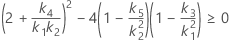
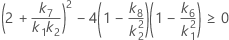
두 조건이 충족되지 않으면 Minitab에서 이 방법을 사용하여 하한과 상한을 계산할 수 없습니다. Minitab에서는 Satterthwaite 근사를 사용하여 하한과 상한을 계산합니다.
Satterthwaite 근사
L과 U가 다음과 같이 정의된다는 점을 제외하고 하한과 상한은 동일한 공식을 사용하여 계산됩니다.
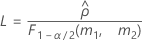
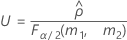
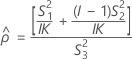
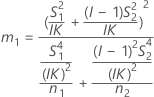
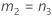
표기법
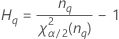
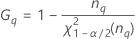
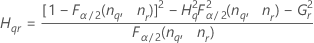
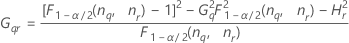
| 용어 | 설명 |
|---|---|
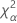 | α * 자유도가 nq인 카이-제곱 분포의 100번째 백분위수 |
| J | 측정 시스템 수 |
| I | 부품 수 |
| K | 반복실험 횟수 |
재현성 분산 및 총 분산의 비율에 대한 신뢰 구간
두 가지 가능한 계산 방법이 있습니다. 첫째, Minitab에서는 수정된 대표본(MLS) 방법을 사용하여 한계를 계산합니다. 계산하는 동안 특정 조건이 충족되지 않는 경우, Minitab에서는 대체 근사를 사용합니다. 단측 신뢰 한계를 계산하려면 H 및 G에서 α/2를 α로 대치하십시오.
MLS 방법
근사 (1–α) * 100% 신뢰 구간의 하한과 상한은 2차 방정식을 풀어 계산합니다.
- 하한
-

- 상한
-

두 번째 방법
B2– 4AC < 0인 경우에는 2차 방정식의 해가 없습니다. 이 경우 Minitab에서는 두 번째 방법을 사용하여 신뢰 구간을 추정합니다. 근사 (1–α) * 100% 신뢰 구간의 하한과 상한은 다음과 같이 계산됩니다.
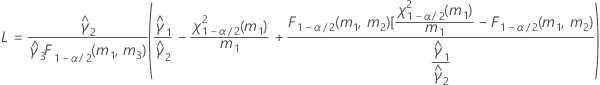
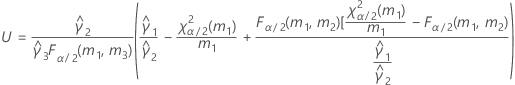
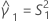
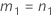
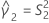
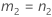

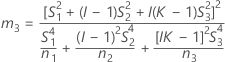
표기법
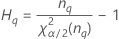
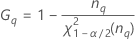
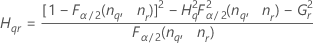
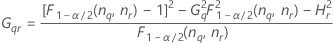
| 용어 | 설명 |
|---|---|
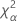 | α * 자유도가 nq인 카이-제곱 분포의 100번째 백분위수 |
| J | 측정 시스템 수 |
| I | 부품 수 |
| K | 반복실험 횟수 |
부품 분산 및 총 분산의 비율에 대한 신뢰 구간
두 가지 가능한 계산 방법이 있습니다. 첫째, Minitab에서는 수정된 대표본(MLS) 방법을 사용하여 한계를 계산합니다. 계산하는 동안 특정 조건이 충족되지 않는 경우, Minitab에서는 대체 근사를 사용합니다. 단측 신뢰 한계를 계산하려면 H 및 G에서 α/2를 α로 대치하십시오.
MLS 방법
- 하한
-

- Upper bound
-

두 번째 방법
B2– 4AC < 0인 경우에는 2차 방정식의 해가 없습니다. 이 경우 Minitab에서는 두 번째 방법을 사용하여 신뢰 구간을 추정합니다. 근사 (1–α) * 100% 신뢰 구간의 하한과 상한은 다음과 같이 계산됩니다.
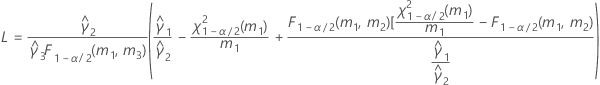
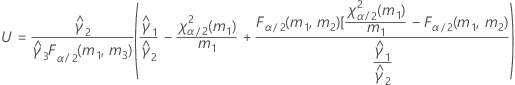

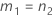

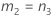

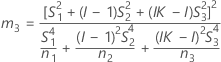
표기법
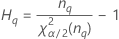
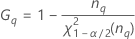
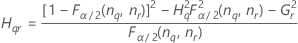
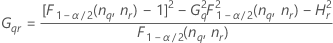
| 용어 | 설명 |
|---|---|
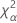 | α * 자유도가 nq인 카이-제곱 분포의 100번째 백분위수 |
| J | 측정 시스템 수 |
| I | 부품 수 |
| K | 반복실험 횟수 |
Gage 분산 및 총 분산의 비율에 대한 신뢰 구간
하한 = 1 – (부품 분산 및 총 분산의 비율에 대한 신뢰 구간의 하한)
상한 = 1 – (부품 분산 및 총 분산의 비율에 대한 신뢰 구간의 상한)