치우침
치우침은 부품의 기준 값과 측정 시스템의 부품 측정값 간의 차이입니다.
공식
각 부품의 평균 치우침:
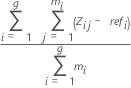
표기법
| 용어 | 설명 |
|---|---|
| zi,j | i번째 부품의 j번째 측정값 |
| refi | i번째 부품의 기준 값 |
| mi | i번째 부품의 반복실험 횟수 |
%치우침
%치우침은 전체 공정 변동의 백분율로 표현되는 치우침입니다.
공식
%치우침 = 100 * (|평균 치우침| / 공정 변동)
표기법
| 용어 | 설명 |
|---|---|
| zi,j | i번째 부품의 j번째 측정값 |
| refi | i번째 부품의 기준 값 |
| mi | i번째 부품의 반복실험 횟수 |
Gage 선형성 및 치우침 연구에 대한 p-값
각 기준 값에서 치우침 = 0인지 여부와 평균 치우침 = 0인지 여부를 검정하려면 p-값을 사용합니다.
p-값은 + |검정 통계량| 오른쪽의 표본 분포 아래 영역과 - |검정 통계량| 왼쪽의 표본 분포 아래 영역으로 정의됩니다. 출력의 p-값은 자유도가 γ인 t-분포와 t-통계량을 사용하여 얻어집니다.
Minitab에서는 표본 범위 방법과 표본 표준 편차 방법에 대한 구체적인 t-통계량 계산을 제공합니다.
표본 범위 방법
Minitab에서는 표본 범위(기본값) 또는 표본 표준 편차를 사용하여 반복성 표준 편차를 추정합니다. 반복성 표준 편차는 t-값을 계산한 후 모든 기준 값과 각 기준 값에 대해 치우침 = 0을 검정하는 p-값을 계산하기 위해 사용됩니다.
공식
표본 범위 방법에서 고유한 각 기준 값이 고유한 부품에 해당하는 경우 반복성 표준 편차는 다음과 같습니다.
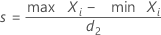
두 개 이상의 부품의 기준 값이 같은 경우, 반복성 표준 편차는 다음과 같습니다.

치우침을 검정하기 위한 t-통계량은 다음과 같습니다.

자유도(γ)는 AIAG 설명서1의 표에서 얻어집니다. Minitab에서는 자유도가 γ인 t 분포와 t-값을 사용하여 p-값을 계산합니다.
표기법
| 용어 | 설명 |
|---|---|
| Xi | 부품의 i번째 측정값의 치우침 |
| d2 | 표1의 값, 표본 크기 = n |
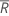 | 평균 범위 |
표본 표준 편차 방법
Minitab에서는 표본 범위(기본값) 또는 표본 표준 편차를 사용하여 반복성 표준 편차를 추정합니다. 반복성 표준 편차는 t-값을 계산한 후 치우침 = 0을 검정하기 위해 p-값을 계산하는 데 사용됩니다.
공식
표본 표준 편차 방법에서 하나의 기준 값이 단일 부품에 해당하는 경우 반복성 표준 편차는 다음과 같습니다.

치우침을 검정하기 위한 t-통계량은 다음과 같습니다.

자유도는 n - 1입니다. 출력의 p-값은 t-분포로부터 t-값과 자유도를 사용하여 얻어집니다.
두 개 이상의 부품의 기준 값이 같은 경우, 반복성 표준 편차는 기준 값이 같은 여러 부품의 합동 표준 편차입니다.

치우침을 검정하기 위한 t-통계량은 다음과 같습니다.

자유도는 (n1- 1) + ... + (ng - 1)입니다. 출력의 p-값은 t-분포로부터 t-값과 자유도를 사용하여 얻어집니다.
표기법
| 용어 | 설명 |
|---|---|
| x | 부품의 i번째 측정값 |
 | 부품의 평균 측정값 |
| n | 표본 크기 |
| S1 | n1개 측정값을 사용한 부품 1에 대한 표본 표준 편차 |
| Sg | ng개 측정값을 사용한 부품 g에 대한 표본 표준 편차 |
