Gage R&R (확장) 연구에 대한 방법 및 공식

Gage R&R (확장) 연구 방법

Minitab에서는 랜덤 효과 모형, 혼합 효과 모형, 내포 설계 모형 등 세 가지 유형의 분산 분석 모형을 일반 선형 모형 접근 방식과 함께 사용하여 Gage R&R 연구를 수행합니다. 랜덤 효과 모형이 기본값입니다. 고정되거나 내포된 요인이 있는 경우 혼합 효과 모형 또는 내포 설계 모형이 사용됩니다.

최종 선택되는 모형에는 주효과 항, 유의한 최고차 항 및 그 사이의 관련이 있는 교호작용만 포함됩니다. Minitab에서는 적절한 모형에 대한 분산 분석표를 계산합니다. 그런 다음 이 표가 Gage R&R 표에 표시되는 분산 성분을 계산하기 위해 사용됩니다.

참고 문헌

Burdick, R. K., Borror, C. M., and Montgomery, D.C. (2003). "A Review of Methods for Measurement Systems Capability Analysis", Journal of Quality Technology, 35(4) 342–354.

Adamec, E. and Burdick, R.K. (2003). "Confidence Intervals for a Discrimination Ratio in a Gauge R&R Study with Three Random Factors", Quality Engineering, 15(3) 383–389.

랜덤 효과 모형

이 명령에 사용되는 기본 모형은 랜덤 효과 모형입니다. 세 요인에 대한 완전 모형을 지정하는 경우:

Y_ijkl = μ + P_i + O_j+ A_k + (PO)_ij + (PA)_jk + (OA)_jk + (POA)_ijk + ε_ijkl

설명:

용어	설명
μ	상수
P_i	i번째 부품

용어	설명
O_j	j번째 조작자

용어	설명
A_k	추가 요인의 K번째번째 수준

P_i, O_j, A_k, (PO)_ij, (PA)_jk, (OA)_jk, (POA)_ijk 및 ε_ijkl은 독립적으로 평균이 0, .

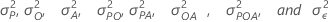Minitab은 일반 선형 모형 적합을 사용하여 분산 성분을 추정합니다. 분산 성분 추정에 대한 자세한 내용은 일반 선형 모형 적합에 대한 방법 및 공식으로 이동하십시오.

부품 항이 부품-대-부품 변동을 계산하기 위해 사용되는 유일한 항인 경우:

총 Gage R&R
반복성
재현성
조작자
A
부품 * 측정 시스템
부품 * A
부품-대-부품
부품
총 변동

참고

사용자가 공정 변동을 추정하기 위해 과거 표준 편차를 지정하면 Minitab에서 다음 작업을 수행합니다.

과거 표준 편차가 데이터에서 계산된 총 Gage 표준 편차보다 크면 총 표준 편차가 σ이고 부품 대 부품 표준 편차가 다음과 같습니다.
그렇지 않은 경우 Minitab에서는 데이터를 사용하여 총 표준 편차와 부품 대 부품 변동을 추정합니다.

부품-대-부품 변동에 대한 항을 더 많이 지정하면 표가 그에 따라 변경됩니다. 예를 들어 부품 요인과 요인 A가 모두 공정 변동을 나타내는 경우 부품, A 및 부품과 A의 교호작용이 부품-대-부품 변동을 추정하기 위해 지정됩니다.

총 Gage R&R
반복성
재현성
조작자
부품 * 측정 시스템
부품-대-부품
부품
A
부품 * A
총 변동

참고

사용자가 공정 변동을 추정하기 위해 과거 표준 편차를 지정하면 Minitab에서 다음 작업을 수행합니다.

과거 표준 편차가 데이터에서 계산된 총 Gage 표준 편차보다 크면 총 표준 편차가 σ이고 부품 대 부품 표준 편차가 다음과 같습니다.
그렇지 않은 경우 Minitab에서는 데이터를 사용하여 총 표준 편차와 부품 대 부품 변동을 추정합니다.

4개 이상의 요인에 대해 Gage 반복성, 재현성 및 부품-대-부품은 3요인의 경우와 유사하게 정의됩니다. 일반적으로 다음과 같습니다.

Gage 반복성 = 오차 항에 대한 분산 성분
부품-대-부품 변동 = 부품에 대한 분산 성분 또는 부품-대-부품 항에 대한 분산 성분의 합
Gage 재현성 = 나머지 항에 대한 분산 성분의 합

혼합 효과 모형

일부 항이 고정된 선형 모형은 혼합 효과 모형입니다. 랜덤 항의 분산 성분은 일반 선형 모형 적합의 결과를 사용하여 얻습니다.

분산 성분 추정에 대한 자세한 내용을 확인하려면 일반 선형 모형 적합에 대한 방법 및 공식으로 이동하십시오.

고정된 항의 경우 분산 성분이 없습니다. 고정된 항 단계 간 변동성은 다음과 같이 추정합니다.

Minitab에서는 선형 모형을 적합하여 요인의 첫 J-1 수준에 대한 계수를 추정합니다.
수준 J에 대한 계수 = –(첫 J-1 수준에 걸친 계수의 합).
추정된 변동성 = 모든 수준에 걸친 (계수)²의 합 / 수준의 수.

혼합 효과에 대한 Gage 재현성 계산에서 고정된 항의 분산 성분은 φ에 의해 대치되지만 랜덤 효과 모형 정의는 유지됩니다.

내포 설계 모형

일부 요인이 다른 요인 아래 내포된 경우, Minitab에서는 일반 선형 모형 적합을 사용하여 모형을 적합합니다. 분산 성분 추정에 대한 자세한 내용은 일반 선형 모형 적합에 대한 방법 및 공식에서 확인하십시오.

Gage 반복성, 재현성 및 부품-대-부품 변동은 랜덤 및 고정 요인의 경우 같은 방식으로 정의됩니다.

Gage R&R (확장) 연구 계산

Minitab에서는 Gage R&R (확장) 연구에 대해 두 개의 표를 표시합니다. 첫 번째 표에는 분산 성분 열과 (분산 성분의) %기여 열이 포함됩니다. 분산 성분 추정에 대한 자세한 내용은 일반 선형 모형 적합에 대한 방법 및 수식에서 확인하십시오.

%기여 = 분산 성분의 값 / 총 변동.

두 번째 표에는 다음 항목이 포함됩니다.

표준 편차(SD) = sqrt (분산 성분)
연구 변동 = 표준 편차의 수 * 표준 편차
%연구 변동(%SV) = 연구 변동 / 총 변동에 대한 연구 변동
%공차 = 연구 변동 / 공정 공차
%공정 = 표준 편차 / 과거 표준 편차

%공차 및 신뢰 구간

%공차는 각 성분에 대한 공차의 백분율입니다.

공차(규격 상한 – 규격 하한)가 지정되는 경우, %공차는 각 성분에 대한 연구 변동을 지정된 공차로 나눠 계산합니다.

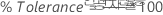
하나의 규격 한계만 지정된 경우 공차 백분율은 각 연구 성분을 단측 공차로 나눈 값의 절반입니다. 단측 공차는 모든 측정값의 평균에서 지정된 규격 한계를 뺀 값의 절대값입니다.

Minitab에서는 사용자가 옵션 하위 대화 상자에 공정 공차(규격 상한 - 규격 하한) 또는 규격 한계를 입력하는 경우에만 이 값을 표시합니다.

L과 U가 분산 성분의 하한 및 상한인 경우 해당 공차 백분율의 신뢰 구간은 다음과 같습니다.

용어	설명
k	k는 연구 상수이며 기본값은 6입니다.

구별 범주의 수

구별 범주의 수는 제품의 변동 범위에 걸쳐 나타나는 겹치지 않는 신뢰 구간의 개수를 나타냅니다. 구별 범주의 수는 측정 시스템이 공정 데이터 내에서 식별할 수 있는 그룹의 수로 생각할 수도 있습니다.

그런 다음, 값이 1보다 작은 경우를 제외하고는 이 값을 절사합니다. 값이 1보다 작으면 구별 범주의 수를 1로 설정합니다.

신뢰 구간

L과 U를 Gage 변동과 총 변동 비율의 하한 및 상한이라고 가정합니다. 구별 범주의 수에 대한 하한과 상한은 다음과 같습니다.

참고

L과 U는 (0, 1)에 포함되어야 합니다. L과 U가 범위를 벗어나는 경우 구별 범주의 수에 대한 하한과 상한이 누락됩니다.

오분류 확률

Minitab에서는 사용자가 하나 이상의 규격 한계를 입력하는 경우 결합 확률과 조건부 확률로 오분류 확률을 계산합니다. 분산 분석법과 Xbar-R 방법을 제공하는 분석의 경우 분산 분석 방법을 사용할 때 결과에는 오분류 확률이 포함됩니다.

결합 확률

부품이 불량이지만 해당 부품을 합격시킬 확률:

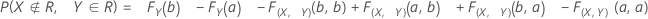
부품이 양호하지만 해당 부품을 기각시킬 확률:

조건부 확률

부품이 불량이지만 해당 부품을 합격시킬 확률(잘못된 합격):

부품이 양호하지만 해당 부품을 기각시킬 확률(잘못된 기각):

표기법

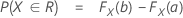
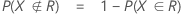
F_(X,Y) 는 이변량 정규 랜덤 벡터 (X,Y)^T의 누적분포함수(CDF)입니다. 설명:

평균, μ = (θ,θ)^T

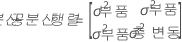
F_(X) 및 F_(Y)는 해당하는 주변 누적분포함수입니다.

즉,

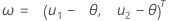
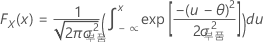
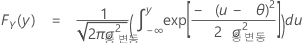
VDA 5에 대한 통계

다음 방정식은 구성 요소에 대한 불확실성을 제공합니다.

해(uRE)
측정 대상의 반복성(uEVO): √(반복성을 위한 분산 성분)
작업자의 재현성(uAV): √(연산자에 대한 분산 성분)
연구 요인의 기여도(u 뒤에 요인 이름): uV_i = √(요인에 대한 분산 성분)
상호 작용(uIA)
다른 요인들(uREST)
측정 프로세스(uMP)

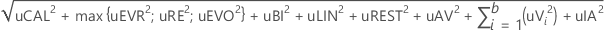
총계의 %

각 구성 요소의 측정 프로세스 백분율에는 다음 방정식이 있습니다.

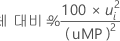
%QMP

공차 백분율 계산은 측정 프로세스로 인한 불확도를 사용합니다.

표기법

용어	설명
n	측정값의 개수
x_i	i^번째 부분의 측정
	n개 측정값의 평균
RE	측정 프로세스의 분해능입니다. 계산에서는 분석 사양에 분해능이 포함된 경우 분해능으로 인한 불확실성을 고려합니다.
x_m	기준 측정값
C_i	상호 작용에 대한 분산 구성 요소
j	통계적으로 유의한 상호 작용 수
F_i	연구에 없는 추가 요인으로 인한 불확실성. 값은 분석을 위한 사양에서 가져온 것입니다.
a	분석 사양의 불확실성에 기여하는 다른 요인의 수
uCAL	교정으로 인한 불확실성. 분석 사양에 값이 포함되지 않는 한 값은 0입니다.
uEVR	기준 값에서의 반복성으로 인한 불확실성. 분석 사양에 값이 포함되지 않는 한 값은 0입니다.
uBI	편견으로 인한 불확실성. 분석 사양에 값이 포함되지 않는 한 값은 0입니다.
uLIN	선형성으로 인한 불확실성. 분석 사양에 값이 포함되지 않는 한 값은 0입니다.
uV_i	연구에 포함된 부품 및 운영자 이외의 추가 요인으로 인한 불확실성
b	불확실성에 기여하는 부품 및 운영자 외에 연구의 요인 수
u_i	불확실성의 단일 구성 요소
k₁	Minitab에서는 표준 정규 분포의 6 표준 편차(기본값)를 사용하여 측정값의 99.73%를 나타냅니다. 이 값을 변경하려면 옵션 하위 대화 상자를 참조하십시오. 예를 들어, 측정값의 99%를 나타내려면 승수 5.15를 사용합니다.